Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.013
弾性力学ないし計算力学を学習する際に最初に出てくる総和規約について説明します。
計算力学で取り扱われる分野では空間をデカルト直交座標系で定義し，その成分を x,y,zで記述することが一般的です。
微小な線分の長さを ds とすると，ds は x,y,z の3成分で構成されます。
これを添え字を使用して表現すると次のようになります。
dx = dx1
dy = dx2
dz = dx3
添え字のことを index といいますが，表現の仕方の違いだけで言わんとしていることは同じです。
ですので添え字で書かれているからといって，別にびびってたじろぐ必要はありません。
微小な線分の長さ ds とその成分 dx , dy , dz の関係は以下のように記述されます。
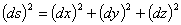
同じことを添え字を使用して記述すると以下のようになります。
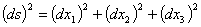
高校で習った総和記号を使用して上記の関係を記述すると以下のようになります。
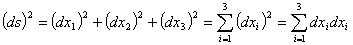
総和記号をいちいち書くとめんどくさいので，1つの項に同じ添え字が2度以上現れるときには，総和記号を省略して記述して表記し，総和を取るというルールのことを総和規約といいます。
つまり「総和規約に従う」と一言ある場合は次のように考えなさいということです。
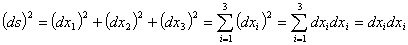
次の表現も上と同じ内容です。
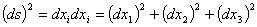（ i = 1,2,3 ）
添え字表現や総和規約について理解するためには，i = 1 , 2 , 3 と代入して紙に徹底的に書き出すことです。
高校の数学では数列という分野が登場します。パズルのような新感覚の分野で多くの人が理解できないまま通り過ぎてしまう分野です。しかしこの分野ができるかどうかは理系に進むにあたって非常に重要な示唆を与えます。
この分野の問題の多くは規則性を見出すことに主眼が置かれています。
規則性を見出すための一般的なアプローチはまず簡単なところから試してみるということであり，
n = 1,2,3 と代入して観察するということです。
これはあらゆる理系の研究活動に取り組む一般的な姿勢であり，まずは試してみるという発想を持ち得ない人や簡単なところから始めてみるという行動を頭だけで馬鹿にして実行に移すことができない人は，特に工学分野では通用しないと考えてよいのではないでしょうか。
必要や興味があって計算力学の添え字表記に出会ったのなら，上記を肝に銘じて地道に 1,2,3 と代入して徹底的に書いてみて下さい。すぐに慣れてしまうと思います。多くの人は添え字表現に慣れることは目標ではなく通過点のはずです。通過点はどんな方法でもよいので早く通過してしまうことです。細かいことはあとで戻ってきてやればよいのです。
