Math and Physics
Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.011
工学では,行列はツールとして頻繁に登場します。しかし,理学部の数学科のように理論を追求しているわけではないので,ツールとして正しく使えるようにすることが重要であり,学習の目的となります。
数値解析の理論的な勉強をしようとすると参考書には行列の演算表記が頻繁に登場しますが,これらの演算を理解するために行列などの参考書を見ても意外と参考にならないことが多いのが現実です。その理由は,数学向けの参考書は数値解析を前提に書かれていませんので,数値解析で頻繁に登場する演算について詳細に説明されていないことによります。
また数値解析の参考書も紙面数の制約と,行列演算は学習済みという前提で書かれています。このとき,参考書によって行列の表記が複数あることに気が付きます。理解してしまえばどれも言っていることは同じということがわかるのですが,大学生で研究室に入ってから勉強しようという初学者からすれば,本題に入る前に混乱してしまいかねません。
そこで,今回は行列の表記と最低限のオペレーションをまとめておこうと思います。
ちなみに数値解析の初学者が行列演算を学習するのに最適な参考書は,
三好俊郎:「有限要素法入門改訂版」,培風館
培風館ウェブサイトはこちら
であると現在筆者は考えています。
この書のよいところは演算を自分自身の手でやったときに,他の同分野の書の助けを借りずにこの本だけで勉強できることです。
演算の説明が多く,自分自身で手計算する場合に分かりやすいと思います。
結局のところ,ツールとして行列演算を学ぶわけですから,頭で理解するのではなく自分の手を動かして身に付けてやろうという姿勢が必要です。その際この書の説明は工学の精神に近いところに位置しており,それが取り組みやすい理由であると筆者は考えています。
参考書を開くと本によって行列にはいろいろな表記があるのがわかります。
これは紙面数の都合やレイアウトの関係といった理由から著者の流儀などが関係していることと思います。
以下に行列 {A} の成分表示に関してよくある表記を記します。内容はみんな同じです。表記が少しずつ異なっているだけです。
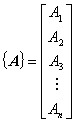
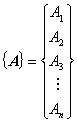
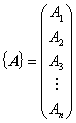
行列の成分表示は縦に記述するのが一般的ですが,紙面スペースの消費量が大きいため,転置オペレーション表記を利用して,次のように記述されることもあります。これらは言っていることは上記の行列成分と同じですが,転置オペレーションを加えて横書きにすることで紙面スペースの消費を抑えています。
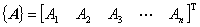
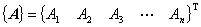
表記が若干異なりますが上記の転置表記について2つは同じ内容です。
転置演算については以下のようになります。成分計算を実際に手を動かして確認することを推奨します。
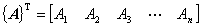
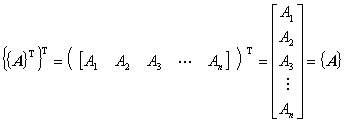
内積は数値解析の定式化において頻繁に登場するオペレーションです。
前述の行列成分の表記の意味が分かっていれば問題なく理解できることと思います。
行列(ベクトル)どうしを内積演算するとスカラー量が得られるということを覚えておくとよいでしょう。