Math and Physics

Non-Linear Solver / Newton-Raphson Method 1

ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.010

４ 上に凸な場合

ここまでは，

(10.1)

を満たす，解を求めてきました。
構造解析では，荷重−変位関係の非線形性を解く場合，Y は 0 でない値になります。
このようなケースについて，Newton-Raphson 法を適用してみます。

図 1 にこのような問題の概要を示します。

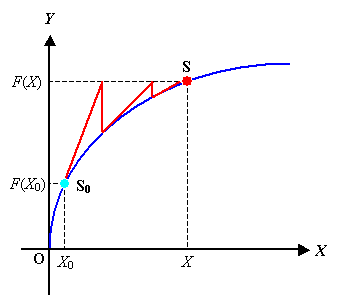
図 1　1 変数問題

この問題は，初期値として我々は関数

(10.2)

にいるとし，ここから，

(10.3)

を満たす X をニュートン・ラプソン法により求めることです。
最初に書いたように，この問題のミソは，Y を与えて，それを満たす X という解を得ようとしていることです。
その逆は，X を与えてそれを満たす Y という解を得ることです。
これは，構造解析では，「荷重制御」か「変位制御」という言い方をされます。
つまりどちらかの値は既知として与える必要があります。
どちらも分からなくなってしまう状態を解析するのは座屈後解析のときです。
今は，座屈のことは考えず関数は単調増加であるものとしておきます。

関数形が既知であるので S₀ より dX₀ 離れた点における関数値はTaylor展開によれば次のように見積もることが可能です。

(10.4)

簡略化のために高次項を無視すると，

(10.5)

となります。 ここで，左辺は目標としている関数値であり，S において

(10.6)

となります。
したがって，X の増分値

(10.7)

より

(10.8)

が得られます。
これにより，初期の解 X₀ よりも dX₀ だけ真解 X に近づいて更新された近似解 X₁ の値が

(10.9)

として得られます。
したがって，関数形が既知であるので直ちに，X₁ に対応する関数値 F ( X₁ ) が求まります。
この点を S₁ とします。
図 2 を見て，我々は S₀ からゴール S を目指して S₁ まで来たことを理解して下さい。
当然まだ S との差（誤差）があり，数値計算でいう解が収束した段階ではなく反復計算中ということになります。
この差が，ユーザーが設定した許容値 ε 以下になれば真解が得られたとみなします。

(10.10)

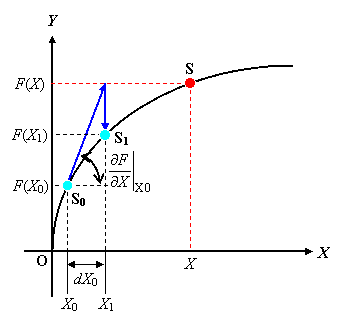
図 2　1 回目の試行計算により S₁ が見出された！

まだ解は収束していませんので，次の近似解を得るべく計算を続行します。
点 S₁ において dX₁ 離れた点における関数値はTaylor展開によれば次のように見積もることが可能です。

(10.11)

簡略化のために高次項を無視すると，

(10.12)

となります。
ここで，左辺は目標としている関数値であり，S において

(10.13)

となります。 したがって，

(10.14)

より

(10.15)

が得られます。
これにより，現在の近似解 X₁ よりも dX₁ だけ真解 X に近づいた近似解 X₂ の値が

(10.16)

として得られます。
したがって，関数形が既知であるので直ちに， X₂ に対応する関数値 F ( X₂ ) が求まります。
この点を S₂ とします。
図 3 を見て，我々は S₀ からゴール S を目指して S₂ まで来たことを理解して下さい。
当然まだ S との差（誤差）があり，数値計算でいう解が収束した段階ではなく反復計算中ということになります。
この差が，ユーザーが設定した許容値 ε 以下になれば真解が得られたとみなします。

(10.17)

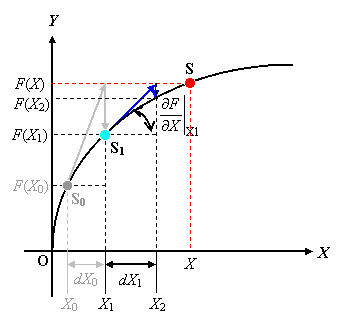
図 3　試行計算により S₂ が見いだされた！

図ではまだ解が求まっていません。
別な言い方をすれば，解は収束していません。
したがって，さらにニュートン・ラプソン法による反復計算を続行していきます。

以上のプロセスにより，解の変化が指定した許容値以内に収まった時点で，解は収束したとみなします。

Copyrights(c) 1999-2004 Kihei Tsutsui All Rights Reserved.