Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.005
差分近似の数式展開について説明します。
前回は，差分法の基礎として，支配微分方程式を差分近似するオペレーションを復習しました。
それは，一階微分方程式の各項を，差分により近似するというものでした。
その際使用した差分はいずれも前進差分と呼ばれるものでした。
今回は，後退差分と中心差分を加えて差分近似の導出方法について復習します。
これは，前回導出しました。
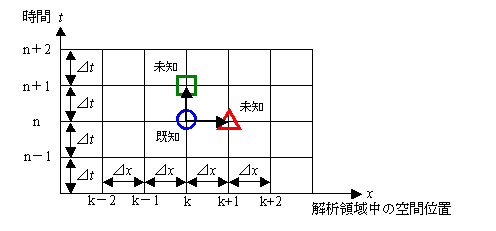
t = n かつ x = k に今自分がいるとします。
この時点で既知な量をもって，時間方向及び空間方向に関して次のステップでの値（未知量）を計算する差分が前進差分です。 ここでは，時間方向については間隔を ⊿t とし，空間方向については間隔を ⊿x とします。
時間微分項を差分で近似します。
まず， 現在の関数値：基準としている時間 t = n と空間位置 x = k での関数値を
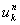
と表記します。
求めたい関数値：基準から ⊿t 後の時間 t = n＋1，空間位置 x = k での関数値を
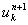
と表記します。
|
(5.1) |
ですので，t についてテーラー展開を考えます。
|
(5.2) |
より，右辺の
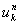
を左辺に移項します。
|
(5.3) |
両辺を ⊿t で割ると
|
(5.4) |
となり，右辺の
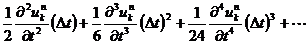
の部分は ⊿t が小さければ
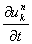
の項に対して無視してもよさそうなので切り捨てます。
したがって，上記テーラー展開は
|
(5.5) |
のように書き改めることができます。
切り捨てた部分は，誤差となり ⊿t が十分小さければ誤差のメインは
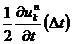
の項となります。
したがって，この差分の精度は ⊿t について 1 次精度であるといいます。
以上より，時間微分項は次のように表現できることがわかります。
|
(5.6) |
空間微分の項も同様にして差分近似してみます。
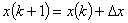
ですので，次のテーラー展開を考えます。
|
(5.7) |
となります。右辺第1項を左辺に移項すると次式のようになります。
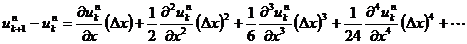
両辺を ⊿x で割ると
|
(5.8) |
ここで，右辺の
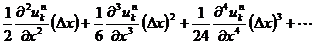
の部分は ⊿x が小さければ，これらの項は小さくなるので切り捨てます。
したがって，上記テーラー展開は
|
(5.9) |
のように書き改めることができます。
切り捨てた部分は誤差となり，⊿x が十分小さければ誤差のメインは
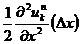
の項となります。
以上より，この差分近似は1次精度であるといい，次のように表現できることがわかります。
|
(5.10) |
上記は時間及び空間に関する1次精度の前進差分といいます。
次に 1 次精度の後退差分を考えます。
後退差分とは，現在（時間 t ( n ) および空間 x ( n ) ）における値（未知量）を，ひとつ前のステップにおける値（既知量）より計算する差分です。下の図を参考にしてください。
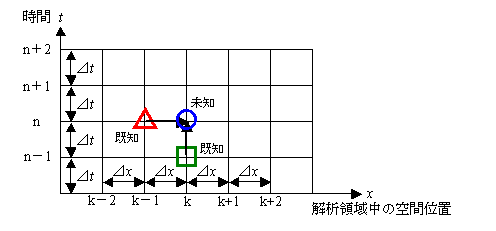
求めたい関数値：基準から ⊿t 後の時間 t = n＋1，空間位置 x = k での関数値を
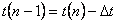
と表記します。
テーラー展開を考えます。
|
(5.11) |
となります。 上の式で右辺の
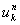
を左辺に移項します。
|
(5.12) |
両辺を－⊿t で割ると
|
(5.13) |
となり，右辺の
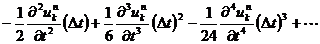
の部分は ⊿t が小さければ無視してもよさそうなので切り捨てます。
したがって，上記テーラー展開は
|
(5.14) |
のように書き改めることができます。
切り捨てた部分は，誤差となり ⊿ t が十分小さければ誤差のメインは
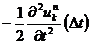
の項となります。
したがって，この差分の精度は ⊿t について 1 次精度であるといいます。以上より，時間に関する 1 次精度の後退差分は次式で表されることがわかります。
|
(5.15) |
空間微分の項も同様にして差分近似してみます。
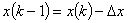
であるから，テーラー展開を考えます。
|
(5.16) |
となります。右辺第 1 項を左辺に移項すると次式のようになります。
|
(5.17) |
両辺を－⊿x で割ると
|
(5.18) |
ここで，右辺の
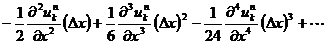
の部分は ⊿x が小さければ無視してもよさそうなので切り捨てます。したがって，上記テーラー展開は
|
(5.19) |
のように書き改めることができます。
切り捨てた部分は誤差となり，⊿x が十分小さければ誤差のメインは
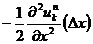
の項となります。
以上より，空間に関する 1 次精度の後退差分は次のように表現できることがわかります。
|
(5.20) |
前進差分や後退差分のように既知量に対して片側の情報を使用して未知量を求める差分を片側差分とよびます。
時間は常に一方向にのみ進む現象であるので，片側差分が使用されます。
空間を一方向に移動していくような現象を差分近似する場合も片側差分が用いられます。
差分という言葉が多く出ていますが，あくまでも工学現象を表現する微分を近似するための手段として用いているに過ぎません。
ここでは，一階微分項の差分近似を取り扱っており，差分としては片側差分を使用してきました。
ここで，空間の一階微分項の片側差分について，次の後退差分と前進差分
|
(5.21) |
について，誤差の項も入れて
|
(5.22) |
を片々加えると，
|
(5.23) |
となり，両辺を 2 で割ると，次の式を得ます。
|
(5.24) |
誤差の主要項は ⊿x の二次式になります。
⊿x を小さく取れば，誤差の影響は片側差分よりも小さくなり，差分近似の精度が高いことがわかります。
⊿x = 0.1 に対して，⊿x2 = 0.01 であることを考えれば想像できると思います。
この差分近似は，誤差の項を無視して，中央差分とか中心差分と呼ばれます。
|
(5.25) |
他にも一階微分項を差分近似するオペレーションがたくさん存在します。
それらに関しては，参考書を読まれることをお勧めいたします。
工学の方程式には，一階微分項のほかに，二階微分項が登場します。
二階微分項の差分近似については，今後取り上げる予定です。
