Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.004
数値計算を指向した差分法に関して，基礎的な部分の勉強について考えてみます。
工学現象はいろいろな先達の努力によって微分方程式で物理モデルを表現することが可能となりました。
この物理モデルを理論解析により厳密に解くことは非常に困難であるので，数値計算手法により計算機を使用して解くことが今日では一般的です。
市販の解析ソフトウェアでは，流体力学や電磁波解析分野では，差分法を用いて解かれることが一般的です。
差分法は，微分方程式の各項を適当な差分で近似して解く手法です。そのため，勉強の第一歩は，微分を差分に置き換える作業を理解することが中心となります。
物理モデルは，求めたい物理量を空間や時間の関数として表現し，その分布を捉えます。これを微分形式で表したものが，支配微分方程式です。例えば輸送方程式とか波動方程式とよばれている微分方程式は次のように表されます。
|
4.(4.1) |
u は時間と空間の位置を変数とするポテンシャルという関数です。時間や位置が変われば，その値は変化します。上記の方程式は，時間が正の実数である範囲で有効となります。時間が負となる現象は，工学問題としては考えられないからです。
この微分方程式を，初期条件と境界条件を与えて解くことが工学の問題です。
先の述べたことと重複しますが，関数は場によって複雑に分布しており，単に微分といっても上記の方程式から，空間及び時間について，厳密な値を求めようと思っても非常に困難です。
そこで，厳密でなくてもよいと割り切って，しかしながらなるべく正確な値が知りたいと発想の転換をします。
その際，微分を差分で近似して解くアプローチが差分法です。
近似ですから，いくらかの誤差があります。
しかしながら，この誤差が 0 に近くなるようにすることで近似解は，厳密解に近づいていきます。
まず次のことを確認してください。
式（4.1）の微分方程式の左辺第1項は，時間微分です。
今の時間を t = ( n )
今より少しだけ後の時間を t ( n－1)
と表現すると約束します。
時間による関数値の変化を評価するためには，同じ場所で時間だけ変えて評価することが必要です。
そのため，関数 u を時間だけで微分する「時間による偏微分」を行っています。
左辺第2項は，空間微分です。
空間微分は，空間における関数値の分布を評価するために必要ですから，これは同じ時間で位置を変えて関数 u を評価する必要があります。
そのため，関数 u を空間座標だけで微分する「空間による偏微分」を行っています。
今空間上で自分のいる位置を x ( k ) とします。
今より少しだけ先の位置を x ( k + 1 ) とします。
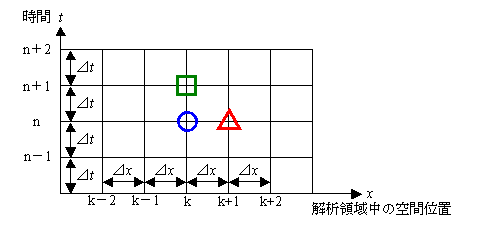
ちょうど下の図のような概念になります。ちなみに上記方程式は，1次元問題ですから，空間といっても x 方向のみを考えればよく，実際には u は，t と x の関数であると考えてよいでしょう。
t ( n ) かつ x ( k ) に今自分がいるならば，下図の○が自分の今いる場所です。
時間方向については間隔を⊿tとし，空間方向については間隔を⊿x とします。
時間微分項を差分で近似します。
まず，
現在の関数値：基準としている時間 t( n )と空間位置 x ( k )での関数値を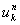 
と表記します。
求めたい関数値：基準から⊿t後の時間 t ( n＋1)，空間位置 x ( k )での関数値を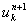 
と表記します。
|
(4.2) |
ここで，テーラー展開を考えてみます。
| (4.3) |
となります。
上の式で右辺の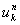 
を左辺に移項します。
|
(4.4) |
両辺を ⊿t で割ると
|
(4.5) |
ここで，右辺の
|
(4.6) |
の部分は ⊿t が十分小さければ
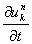
の項に対して無視してもよさそうなので切り捨てます。
したがって，上記テーラー展開は
|
(4.7) |
のように書き改めることができます。切り捨てた部分は誤差となります。誤差のメインは
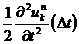
であり，⊿t が十分小さければ上記の誤差は無視してもよさそうです。
Error（⊿t）は切り捨てた項のことです。
「十分小さければ」や「無視してもよさそう」という表現に注意してください。
この判断はあくまで人間が下すということです。
問題によってその度合いは異なるでしょうし，人間によっても気にする人と許容する人に分かれます。
つまり結果はひとつではありません。
もともと近似なのですから。
以上より，時間微分項は次のように表現できることがわかります。
これは時間項の前進差分近似です。
|
(4.8) |
空間微分の項も同様にして差分近似してみます。
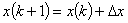
であるので，テーラー展開を考えます。
|
(4.9) |
右辺第1項を左辺に移項すると次式のようになります。
|
(4.10) |
両辺を ⊿x で割ると
|
(4.11) |
ここで，右辺の
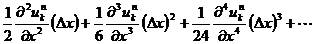
の部分は ⊿x が十分小さければ
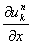
の項に対して無視してもよさそうなので切り捨てます。
したがって，上記テーラー展開は
|
(4.12) |
のように書き改めることができます。Error ( ⊿x ）は切り捨てた項を意味しています。
切り捨てた部分は誤差となり，誤差のメインは
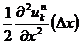
の項となります。
以上より，空間微分項は次のように表現できることがわかります。
|
(4.13) |
したがって，微分方程式の差分近似は次の式となります。
↓
|
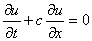
(4.14) |
以上は最も簡単な差分近似の例ですが，オペレーティングの本質はつかめたと思います。
今回の例のように，現在と現在より先の点を用いた差分を前進差分といいます。
また誤差が ⊿t および ⊿x に依存しているので，1 次精度の差分といいます。
以上のように，差分近似の導出は テーラー展開さえ知っていれば，高校生でもできる程度の話です。
現実には，大学生のほとんどは差分近似ができませんが。
学校では，テーラー展開は数学の必修科目で，差分近似は数値解析の選択科目で学ぶことになると思います。
しかしながら，数学の基礎科目の大半は数学科の教官によって講義されます。
工学ではオペレーションの習得がまず重要です。
なぜなら数学は手段であると考えるからです。
理学部数学科の教官には，このような背景を汲み取って，工学部の学生の講義では理学部の学生相手の講義とは切り替えるという配慮が全くありませんでした。
ロボットのようにだれが目の前で聞いていても同じ内容で同じ単調さで講義を毎年繰り返します。
実際学生の多くは出席をとり終えると教室を後にしてしまいます。
残った人数は最初に100人とすれば5人くらいなもんでしょう。
現在の大学では 1，2 年次の教養課程（今は呼び名が違うだけで中身は今までと同じです)では，ほとんどがこのような講義で占められており，選択の余地とか講義レベルの改善などという呑気なレベルではありません。
ほとんど教育崩壊の様相を呈しており，この講義に当たっている教官すべてを大学から排除しても日本の学生の学力レベルに影響は与えないでしょう。なぜなら，今でもほとんどの学生は講義を聞いていないのですから。
実際には私はすべての教官の存在を否定はしたくはありません。
中には本当にすばらしい誠実な人もいました。
そのような先生から受けたエネルギーは本当に大きいものでした。
しかしながら， 無能で私欲の強い強欲な大学を食い物にしている多くの人間達により，学生が本当に求めている先生方が非常に肩身の狭い思いをしています。それでもよいというのならこの国の行く末も決まったというべきでしょうか。
差分は数値解析の選択科目で習うと思いますが，残念ながら私の場合は低質な講義しかできない教官であったので結局講義は聞きませんでした。今ではその教官は不祥事が表沙汰になり大学の表舞台から去ったと聞いています。ふざけた話ですがこれが日本の惨状です。
講義が時間の無駄であると判断したので，書物で勉強するようにしました。しかしながら，差分近似やテーラー展開の表現が，書物によってまちまちで解釈には非常に苦労しました。今にして思うと，わかってしまえば何が初学者にとってネックとなっているかがわからなくなってしまいます。
数学的なことよりもそのことが差分の勉強において，入口にある最大の壁と思います。
今回の説明が少しでも理解の助けになれれば幸いです。
