Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.006
電磁気学や流体力学あるいは力学などを勉強したり，市販ソフトを使用して解析をしていくにつれて，座標系の知識がかなり必要となることに皆さんうすうす気がついてきます。
物理学などでは，2次元空間を平面ではなく曲面として捉える状況が多くなります。
多くの人は，2次元空間を直感的に平面で捉えてしまう癖がついています。
そのため曲面を2次元で表現する記述に出会うと理解が難しくなってしまうようです。
また有限要素法は，任意形状の物体や空間を要素に分割して各要素ごとに物理量の相互作用を計算します。
このとき，微分や積分が必要になります。微分や積分は常にその対象領域の座標系に対応した形で行われますので，座標系に関するイメージが曖昧であるとその後の理解がすべてあやふやになります。
もうひとつは，市販ソフトを利用していて，局所座標系を使用したい場合やメッシュや形状作成において局所座標系を定義する場面が考えられます。
前者は，理論的な学習や自分で定式化を行ってプログラムを作成する場合に必須になります。
後者は，市販ソフトを高機能に利用する際に必須となります。
つまり，FEMに関係する人は遅かれ早かれ座標系の知識やイメージを理解しておくことが必要とされます。
しかしながら，座標系のイメージがあいまいな人が多く見られます。
そこで，今回と次回の 2 回に分けてFEMを利用する立場から座標系について説明します。
今回は座標系のイメージに関して説明します。
我々人類は，
立体空間を 3 次元という世界の形で想像することができます。
面を2次元の世界として理解できます。
線を1次元の世界として理解できます。
そして，点は 0 次元の世界として理解できます。
ここで，「＊次元」は次のように簡潔にまとめられます。
x , y , z といった 3 つの座標で表現されます。
球とか直方体といった立体はすべて 3 次元空間の世界です。
3次元空間のある一点を指定するためには， x , y , z の 3 つの変数を決める必要があります。
r , θ , z からなる円筒座標は局所座標系の代表のひとつといえます。
x , y といった 2 つの座標で表現されます。
円とか四角形といった平面をふくむ曲面はすべて 2 次元空間の世界です。
2 次元空間のある一点を指定するためには，座標系を構築しているxとyの2つの変数を決める必要があります。
x 座標で表現されます。
直線を含む曲線は 1 次元空間の世界です。
1 次元空間のある 1 点を指定するためには，変数 x を決める必要があります。
点のことです。
点は固有の座標系を持たないことがわかります。
点は 1 次元以上の世界に存在して初めて位置が決まります。
我々が常に使用している座標系で x - y - z と表示されているものは、デカルト直交座標系という 3 次元空間の座標系です。
3 次元空間で何かひとつ標準的な座標系を定義しておかないと，話がまとまりません。
世界共通言語みたいなものと思えばよいでしょう。
このデカルト直交座標系は全体座標系とか Global Coordinates System (グローバルコーディネイツシステム)などと呼ばれます。
しかしながら，我々は時として全体座標系を離れて別の空間を定義し議論を展開するほうが都合がよい場合があります。
全体座標系の中に，別の空間を定義する局所座標系 Local Coordinates System（ローカルコーディネイツシステム)を埋め込むわけです。
都合のよいところは局所座標系を使って考えておいて，結果を全体座標系へ変換すればよいのです。
ですから局所座標系と全体座標系間の変換さえ確立されていれば、積極的に局所座標系を考えてよいのです。
オペレーションは結果が得られれば何でも良いのです。
すなわち，問題を常に直交デカルト座標系で考えることに縛られる必要は全くありません。
今回は
１：プリプロセッサの使用で要求される局所座標系
２：対称境界条件の設定に必要な局所座標系
３：3 軸を正確に定義する局所座標系
についてオペレーションを説明します。
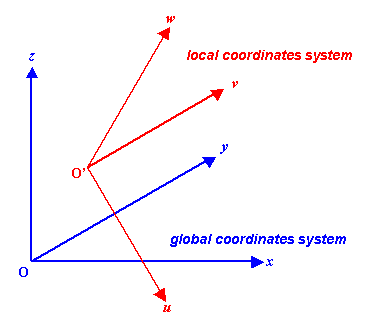
xyz 軸からなる座標系を全体座標系とすれば，uvw 軸からなる座標系を局所座標系と考えることができます。
プリプロセッサを使って，ラインやメッシュ作成時に，回転動作を行いたいときがあります。
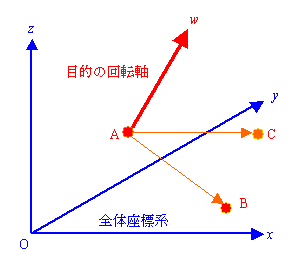
ある任意の軸周りの回転動作を実現するためには，まず回転軸を決める必要があります。
これは一般に，回転軸に対して直交する平面 S を座標 A , B , C を決めることで定義します。
①ベクトル AB を始点座標 A と終点座標 B を与えて定義します。
②ベクトル AC を始点座標 A と終点座標 B を与えて定義します。
③ベクトル AB とベクトル AC より平面 S が定義されます。
④定義された平面 S に対して垂直方向に w 軸が定義されます。この w 軸が回転軸になります。
目的は回転軸 wを得ることであるので局所座標系の u および v 軸を正確に定義する必要はありません。
すなわち，座標 B と C は，平面 S を定義するためのものであり，ベクトル AB および AC は局所座標系の座標軸 u と v を決めるものではありません。
よって目的の w 軸を作れれば座標 A , B , C は自由に設定することが可能です。
円筒形状の解析モデルで，要素数が多い場合，計算時間を削減するために 1 / 4 モデルを作成することがよくあります。
この場合，対称面を全体座標系の座標軸に合わせて設定することが可能なので，対称面上の境界条件の設定は容易です。
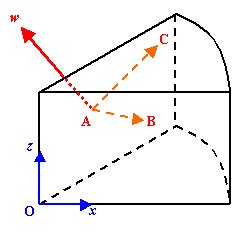
しかしながら，要素数が非常に多く 1 / 4 モデルでは計算時間が許容できない場合に，1 / 8 モデルや 1 / 12 モデルなどが作成されます。
これはショートケーキのような形状をしており，2 面ある対称断面のうち 1 面は全体座標系の座標軸に合わせることができますが，
もう 1 面は合わせることができません。
そのため，この面には局所座標系を定義して，境界条件を与えることになります。
この場合の局所座標系で必要な情報は，対称面の法線方向です。
そのためオペレーションは，プリプロセッサで必要な回転軸を求めたのと同じです。
局所座標系の 3 軸をすべて正しく設定しなくてはならないこともあります。
その場合の代表的なオペレーションは次のものがあります。
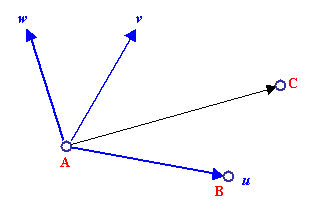
① 始点座標 A と終点座標 B を結んでベクトル AB を作成します。この AB を局所座標系の u 軸とします。
② 始点座標 A と終点座標 C を結んでベクトル AC を作成します。
③ ベクトル AB と AC の外積ベクトルを w 軸とします。
④ u 軸と w 軸の外積ベクトルを v 軸とします。
この方法はいわゆる右手系とよばれる座標系定義の方法です。
以上で座標系の 1 回目を終わりますが，上記の直感的なイメージがあればソフトウェアを使うにはとりあえず困らないと思います。
