
 Math and Physics
Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.003
2010/10/17
連続の式の説明中に出てくる式の表記にミスがありましたので以下の部分を修正しました。
⊿M [kg/m3s] は微小直方体内での質量流量の変化量を意味しているので,次のように表現できます。
の下4行目の式
ご指摘いただいた読者の方、ありがとうございました。
今回は流体力学で登場する連続の式について考えてみます。なお連続の式は,流体力学における発散を表す式です。
連続の式は流体解析で登場します。
一般的な流体解析では,連続の式と Navier-Stokes の式を連成させて解くことで,圧力と流速を求めます。
したがって,連続の式を理解することは流体解析を理解する上で極めて重要です。
また,流体解析を必要としない人も,工学を学ぶならば流体の基礎概念として知っておくことが望ましいと思います。
なぜならば,連続の式は,流体の発散を表す式であるので,発散という概念を通して電磁場や応力の釣り合い,熱量保存というように,他の分野を含めて共通の認識の上で工学現象を理解することができるようになるからです。
まず,連続の式とは何を意味しているか理解することが大事です。
結論から述べると,先に述べたように,連続の式とは,空間中の何もないところから勝手に流体が湧き出して出現したり,吸い込まれて消えてしまうようなことが無いことを定義しています。
すなわち,流体の発散を表わし、流体現象において無から有が生じることはないということを言っています。
このことは,流体の質量保存より導かれます。流体は固体に比べると自由に形を変えられるので変形,分離,結合が容易です。
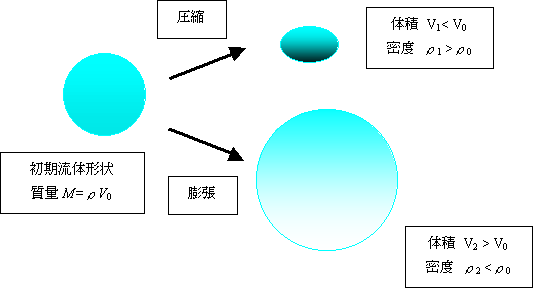
しかし,初期の流体の質量と,変形,分離,結合後の流体の質量を比べると常に同じになります。
これは質量保存則より自明です。
圧縮性流体でも質量は変わりません。変わるのは体積と密度です。
しかし,流体の質量は変わらないので体積が膨張すれば密度が小さくなり,体積が収縮すれば密度が大きくなります。
このことは,直感的にも容易に理解できるでしょう。
そこで,流体力学の連続の式を流体中に仮想的に微小直方体を考えて検討します。
微小直方体の1辺の長さをdx,dy,dzとします。
このとき,x軸,y軸,z軸に垂直な面について流入する流量と流出する流量を考えます。
質量ではなくて,流量というものを考えるのが流体力学のミソなところです。
流量には,以下に示すように体積流量と質量流量の2つがあり区別します。
微小直方体について考えるならば,
体積流量とは,単位時間当たりに微小直方体の各面を通過する流体の体積のことをいい,単位は[m3/s]となります。
質量流量とは,単位時間当たりに微小直方体の各面を通過する流体の質量のことをいい,単位は[kg/s]となります。
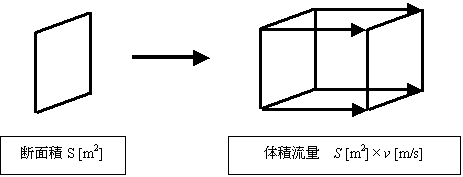
まず,流体の断面積を S [m2] とします。
当たり前ですが,流体の断面積 S [m2] を定義しても体積 V [m3] は定まりません。
そこで流体の速度(流速)v [m/s] を考えます。
今,断面積 S [m2] に垂直方向の流速が v [m/s] であるとすれば,単位時間(1秒間あたり)にこの断面( S [m2] )を通過する流体の量(体積流量)は,
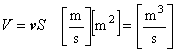
と表わされます。
体積流量 V [m3/s] に流体の質量密度 ρ [kg/m3] をかけると質量流量 M [kg/s] を得ます。
流量について説明したので,連続の式の導出を行います。
まず,微小直方体のx軸方向の流速について,
流入する際の流速の x 方向成分を Vx とすると,流出するときの流速はテーラー展開の1次近似より
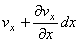
と表すことができます。
y 軸方向および z 軸方向の流速の扱いも全く同様です。
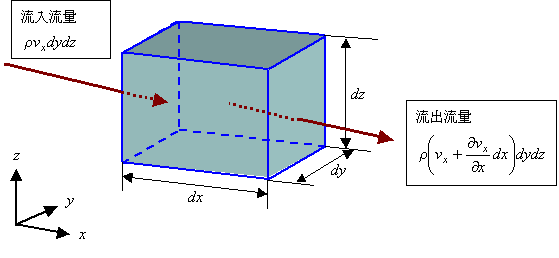
上の図では x 軸方向成分のみ示してありますが,実際には y 軸方向,z 軸方向の流れが存在します。
ただし,考え方および表現式は x がそれぞれ y および z となるだけで全く同じです。
流入時の流速は,
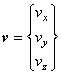
流出時の流速は,検査領域が微小直方体であるのでテーラー展開の1次近似より
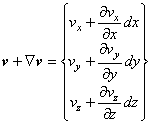
と表せます。
したがって,微小直方体に流入する流体の質量流量は,
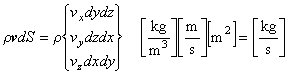
であり,流出していく質量流量は,
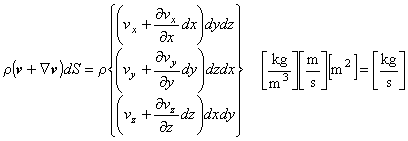
と表せます。
微小直方体に流入する質量流量と流出する質量流量の差を⊿M とすると,
流入は x,y,z 軸に垂直な面から起こるものとし,
流出はそれぞれ反対側の面から起こるとすれば,次の式で表されます。
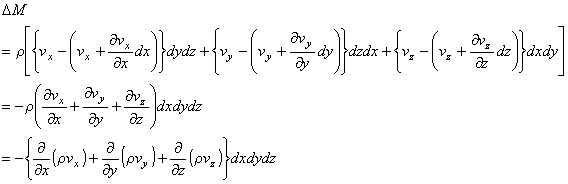
⊿M [kg/m3s] は微小直方体内での質量流量の変化量を意味しているので,次のように表現できます。
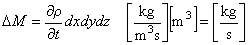
したがって,
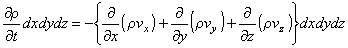
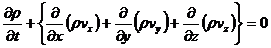
という関係が得られます。
圧縮性流体では,流体の密度は場所によっても,時間によっても変化することが予想されます。
したがって,流体の密度は空間と時間の関数となるので,空間の偏微分と時間による偏微分の影響を受けることになります。
以下に 圧縮性流体の連続の式を示します。
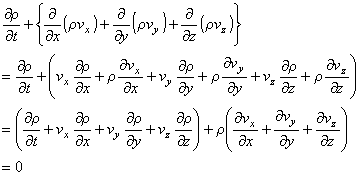
続いて,非圧縮性流体の場合,密度は変化しないため一定値となります。
したがって,密度を時間や空間で偏微分すると0となります。
このことから,非圧縮性流体の連続の式は次のように表されます。
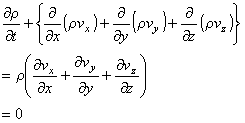
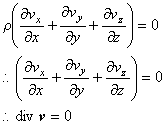
以上より非圧縮性流体について流速の発散が 0 ということが導かれました。
流速の発散が 0 ということは,空間中のある点で流速の湧き出し(吸い込み)量が 0 ということです。
流速の湧き出し(吸い込み)量が 0 ということは,流速が連続であることを意味しています。
流速が連続であるということは,流体粒子の運動が連続体としてモデル化できることを示しています。
そしてなにより重要なことは,
流体が何も無い空間中から勝手に湧き出してきたり,
何も無い空間中で突如消えたりするという,
いわゆる「無から有を生じる」ことは無いということです。
以上で連続の式の説明を終わります。
何も書かないと素っ気無いので,一言。
筆者は学部生の時全く流体力学の講義を聴いていませんでした。
なぜなら自分にとっては全くつまらない講義だったからです。
教科書を丸写しするだけの講義だったと思います。
講義開始時には100人くらいの学生が教室にいますが,そのほとんどは出席をとるためだけに来ていました。
そしてまじめに講義を聴いている人は5人もいなかったのではないでしょうか。
今思うと、各自教科書を読めば済むことなのに,出席確認をするなどというくだらない管理のために
時間の無駄な講義に大勢の学生が時間を拘束されていました。
出席確認のために学生が教室にいるため,
本来出席を取らなければ学生を集められないダメな講義がカモフラージュされている点を強く危惧します。
そのため教育力の不足している教官が大勢教育現場に残り続けています。
確か大学の学則で,授業回数の3分の2以上の出席がないと試験が受けられない制度だったと思います。
はっきりいって馬鹿げています。
高等教育機関が,学生の出席を制度を作って管理しようという発想が何故出てくるのか理解できません。
大学でどうやって勉強するか、そんなことは個人の自己責任に任せればよいと思います。
どうしてそういう発想ができないのでしょうか。
100人分の名前を呼ぶのに5分も10分も時間を費やしている教授ほど情けない姿も無いものです。
そしてその出席確認が終わると大勢の学生が教室から消えていきました。
中には教室から出ていった学生を一生懸命追いかけていって連れ戻そうとしたすごい教官もいました。
そんなことする前に,自分の講義内容で学生を教室に惹きつけていただきたいものです。
しかしながら,出席を取る教官ほど講義のレベルは極めて粗末な傾向にあり
講義の質が高くて面白かった教官ほど,出欠確認など取らなかったことを記しておきます。