円板の非定常熱伝導問題の理論解について
１　概要
　本例題の理論解は，
矢川元基：「有限要素法の基礎と応用シリーズ8　流れと熱伝導の有限要素法入門」，培風館，p.120-121 [1]
に掲載されているものを使用しました。
　 計算コードの動作を確認するためには，この理論解をエクセルや簡単なプログラムを作成して求める必要があります。
しかしながら，上記の文献にある理論解は，複数のベッセル関数[2]を含む複雑な級数となっています。
そのため，簡単に計算することはできません。
ここでは，まず理論解を計算することを最終目的とし，いくつかの段階を経てそこに到達する過程を説明します。
2　理論解

理論解は次式で与えられます。

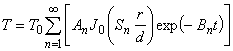
ここで各成分やパラメータは次の表１に示すとおりです。

表１　理論解の各成分及びパラメータ

T0
[℃]
初期温度
r
[m]
半径方向の座標
R
[m]
円板の半径
t
[sec]
時間
Sn 　 0次のベッセル関数　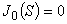 　の解
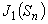　 1次のベッセル関数値
　 　
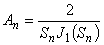λ
[W/m℃]
円板の熱伝導率
ρ
[kg/m3]
円板の質量密度
ｃ
[J/kg℃]
円板の比熱
　 　
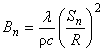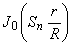　 0次のベッセル関数値

　

3　ステップ１ <0次ベッセル関数の求解>
はじめに，0次のベッセル関数

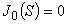
の解を求めます。 ここで，0次のベッセル関数は次式で表されます。

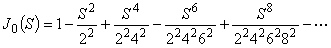（式１）
0次ベッセル関数は無限級数であるので，すべての項を考慮することは不可能です。
そこで，何項までを考慮すればよいか知る必要があります。
今回の目的を，「熱伝導問題の理論解として十分な精度を持たせること」とすれば，その目的を達成できるのに十分な項数を考慮すればよいことになります。
そのためには，まず上記ベッセル関数のグラフを，いくつか項数を決めて作成し，関数形状を把握して検討する必要があります。
読者の方は実際にこの級数のグラフを作成することをお勧めします。
この作業自体が，結構面倒くさい作業であることがわかるはずです。
図１に0次ベッセル関数のグラフを示します。

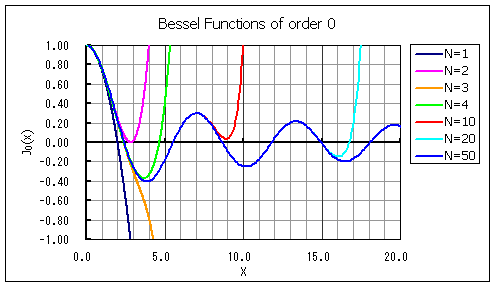
図１　0次ベッセル関数の項数による比較
Nおよび関数形については表２に示すように定義しました。


表２　０次ベッセル関数の項数と関数形

N=1
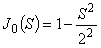N=2
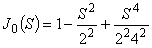N=3
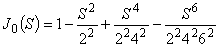N=4
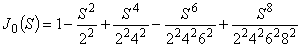N=k

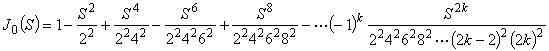図１のグラフより，N=50を正解と仮定すれば，x=20までの範囲には J0(X) = 0 の解は少なくとも6つ存在することがわかります。
ここでは，X をどの領域で考慮すればよいかはわかりませんが，大胆に X = 20.0 までの範囲で考えてみることとし先へ進みます。
したがって，X の範囲の選定が妥当であるかはここではわかりません。

N=1,2,3では，N = 50 とフィットする解は得られていません。
したがって，項数が不足していて不適と判断することができます。
N = 4 では，N = 50 とフィットする 1 つ目の解だけが有効解とみなすことができます。
N = 10では，N = 50とフィットする 2 つ目までの解を有効解とみなすことができます。
N = 20では，N = 50とフィットする 5 つ目までの解を有効解とみなすことができます。
以上より，まず N = 20 を採用し，その 5 つの解を求めることにします。

ここでは，0次ベッセル方程式が 20 次の多項式になりますので簡単に手計算で解を求めることはできません。
数値計算的には，解の範囲がわかっているので2分法を使用して，解を判定することが可能です。
これはかなり工学的な方法ですが，目的は軸対称問題の理論解を得ることにあるのでそれができるのであれば問題ありません。
今回は小数第4桁までの精度で解を求めることにしました。
表３に今回計算により求めた０次ベッセル関数の解について示します。
また日本機械学会から出版されている伝熱工学資料p.35[3]に掲載されている値も同時に示しておきます。


表３　０次ベッセル関数の解

Sn
0次ベッセル関数の解（ N = 20 ）
伝熱工学資料p.35 [3]
S1
2.404 85
2.404 83
S2
5.520 05
5.520 08
S3
8.653 75
8.653 73
S4
11.791 55
11.791 53
S5
14.938 85
14.930 92
今回は2分法により簡単に近似解を求めて済ませていますが，数値計算による多項式の解を求める手法である「デュラン・ケルナー・アバース法」[4]を使用して解を求めることもできます。
この方法は，多項式の解を一度に計算する方法です。
有限要素法だけやっているとこのような計算手法などとは無縁になりがちですから，こういう機会があるときには目先の手間を考えずに果敢にトライしてみることも大事だと思います。といいながら，今回筆者はこの方法にはトライしていません。
4　ステップ2　<１次ベッセル関数の項数の確認>
理論解の式では，０次のベッセル関数の解を使用して１次のベッセル関数値を要求しています。
１次のベッセル関数も無限級数であるので，ここでは関数の計算に先立ち何項まで必要とするか見積もってみます。
１次のベッセル関数は次式で表されます。
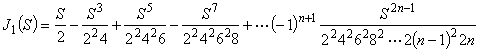　（式２）
この級数展開に必要な項数については，直感的に０次ベッセル関数と同次にするということが考えられますが，一応０次ベッセル関数のときと同じように，項数を変えて関数を再現し，必要な精度があるかどうかをチェックしてみます。
N = 50 項まで採用した関数値を正解と仮定した場合，N = 20 項まで採用した関数値は X = 15 程度まで精度を維持しているとみなせます。
これは 0次ベッセル関数の時と同じ傾向を示しており，1次のベッセル関数についても項数は20とすればよいことが言えそうです。
したがって，1次ベッセル関数の項数は 20 とします。


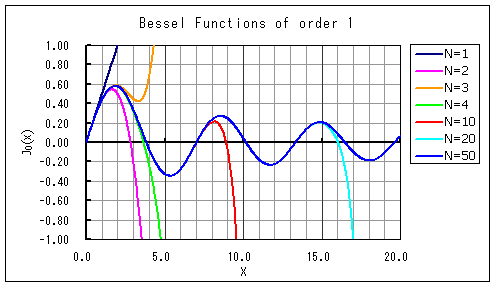
図2　1次ベッセル関数の項数による比較
N および関数形については表４に示すように定義しました。


表４　１次ベッセル関数の項数と関数形

N=1
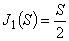N=2
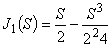N=3
N=4
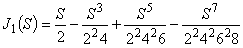N=k

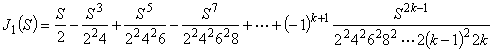5　ステップ 3　<１次ベッセル関数値の計算>

ステップ２で，１次ベッセル関数に必要な項数の把握が済んだので，ここでは１次ベッセル関数の値を計算します。
理論解に現われる１次ベッセル関数は
です。
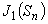
ここでは変数が，０次ベッセル関数の解です。
表5に，0次及び１次のベッセル関数の項数を 20 とした場合の，１次ベッセル関数値は次のようになります。


表5　１次ベッセル関数値
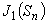１次ベッセル関数の値（ N = 20 ）
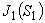0.5191422206
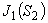-0.3402665392
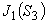0.2714516070
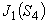-0.2324598170
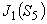0.2018558003
6　ステップ4　<Anの計算>
１次ベッセル関数の値が求められたので，次にAnを計算します。
Anは次式で定義されます。
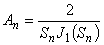　（式３）
これは上の式より容易に計算できます。表6に計算結果を示します。


表6　Anの計算結果
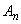計算値
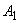1.6019746969
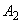-1.0647992584
0.8513991923
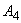-0.7296443220
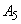0.6632406404

　
7　ステップ5　<Bnの計算>
続いて，Bnの計算を行ないます。
Bnの計算もAnと同様で得られたSnから容易に行なうことが可能です。
Bnの計算式は，文献 [1] では，
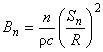
と記述されていますが，この計算式では答えが大きく異なることから，これは誤植であると考えられます。
上記の記述のままですと，理論解の式に熱伝導率が導入されず不自然であると考えられます。
そこで，今回は上式を下記の式に改めて計算しました。
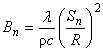　（式４）
得られた結果を表7に示します。

表7　Bnの計算結果
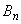計算値
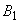0.0000735805
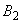0.0003876908
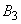0.0009528000
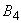0.0017690343
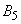0.0028394159
8　ステップ6　<温度の求解>
ステップ １ から 5 までに得られた結果及び知見を考慮して式 （1） により温度分布を計算します。
時間は，1時間後 （3600[sec]） および 2 時間後 （7200 [sec]） の2種類について計算しました。
図３に，計算結果をグラフ化したものを示します。


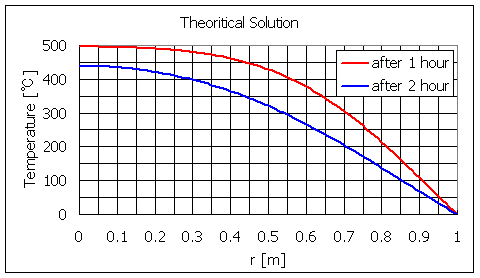
図3　理論解による温度分布

最後に図4にベッセル関数の項数を20と50とした場合について温度分布を示し，理論解を比較します。
両者は少数2桁までほぼ一致し，グラフ上ほとんど一致しています。
つまり，今回は項数を20と仮定しましたが，この項数でも熱伝導問題の理論解として，計算プログラムの動作確認程度の目的には十分な精度を持っていることいえます。


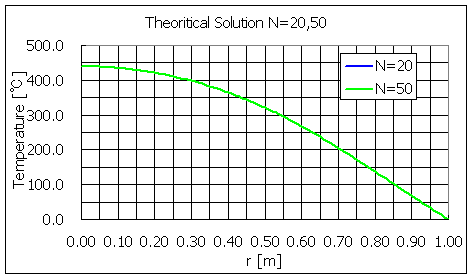
図4　ベッセル関数の項数による理論解の比較

参考文献

[1]　矢川元基：「有限要素法の基礎と応用シリーズ8　流れと熱伝導の有限要素法入門」，培風館，p.120-121
[2]　例えばMurry R. Spiegel 著，氏家勝巳訳：「マグロウヒル数学公式・数表ハンドブック」，オーム社，p.136-145
[3]　日本機械学会：「伝熱工学資料　改訂第4版」，丸善，p.35
[4]　森　正武：「FORTRAN77数値計算プログラミング（増補版）」，岩波書店，p.215-235