例題１１　円柱の軸対称非定常熱伝導解析（熱伝達問題）
出典：日本機械学会：「伝熱工学資料」，丸善，p.34
軸対称／非定常／線形／問題
節点数：306　要素数：500 （三角形環状１次要素）　時間増分値 2.0 [sec]／完全陰解法
境界条件：
連続境界条件＝断熱境界条件：領域上端（ z = 0.05）下端（ z = 0.00）
熱伝達境界条件：右端（ r =1.00）：周囲流体温度 80.0 [℃]，熱伝達係数：5000.0 [W/m2]

物性値：熱伝導率：26.20 [W/m℃]　比熱：439.00 [J/kg℃]，密度：7740.0 [kg/m3]

寸法：Lr = 1.00 [m]　Lz = 0.05 [mm]
解析モデル　（ 軸対称モデル ）

図１に示すような，初期温度が0.0 [℃] 一様であるz方向に無限に長い円柱の断面を考えます。
この断面は左端が対称軸であり，円柱の外部は一様温度80.0［℃］の流体に接しています。
円柱と流体間で熱伝達が起こる条件で，非定常解析を行い円柱の温度を計算します。
円柱はz軸方向に無限に長いので，この方向については温度変化は一様であるとみなせます。
そこで z 方向は適当な部分で打ち切って，断熱境界条件を設定します。
計算は，時刻0.0 [sec]から28800.0 [sec] （8.0 [h]）まで完全陰解法により計算し，理論解と比較します。

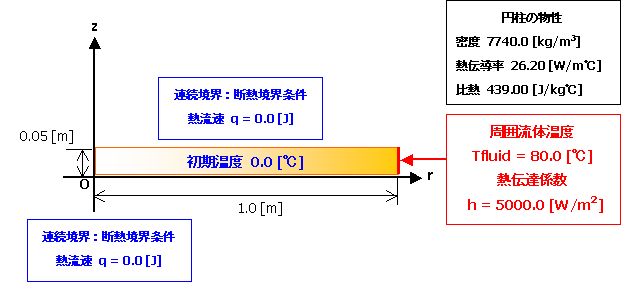
図１　解析モデル
計算結果　温度分布

図２　温度分布アニメーション　（8コマ　1時間ごと）

　

図 2-2 LS-DYNA による計算結果 10コマ

LS-DYNAに関する解析技術のご相談はこちらへ：ランスモア

温度分布グラフ

本例題は，r方向にのみ温度分布が変化する一次元問題です。
本例題の理論解は次の式で与えられます。

■円柱温度

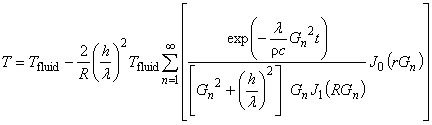
ここで，各変数及びパラメータは次のようであります。

Tfluid

［℃］

 周囲流体温度
r
[m]
 半径方向の座標
R
[m]
 円柱の半径
t
[ t ]
 時間
Gn 　 ベッセル関数を含む方程式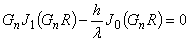



の解
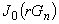　 0次のベッセル関数値
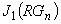　 1次のベッセル関数値
h
[W/m2]
円柱の熱伝達率
λ
[W/m℃]
円柱の熱伝導率
ρ
[kg/m3]
円柱の質量密度
c
[J/kg℃]
円柱の比熱
　

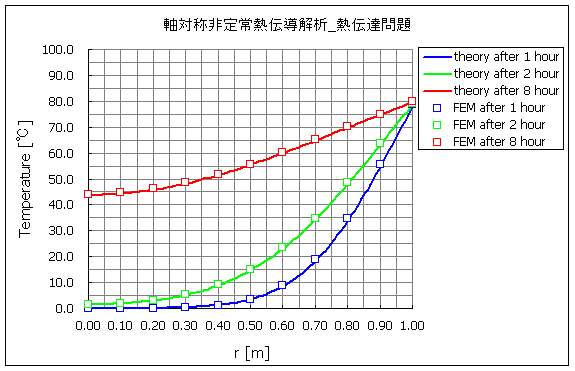
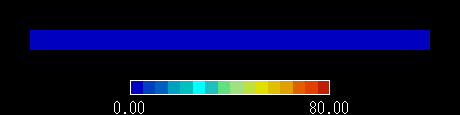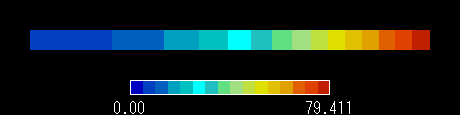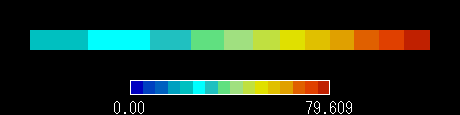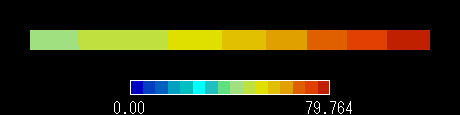
図３　r [m] における温度分布

図3より，計算値は理論解に対して良好な精度を示しています。
理論解は，伝熱工学資料に数表が示してありますのでそれを参考に，上記の関数を計算し求めることができます。
計算ステップ数は，終了時間を8時間＝28800 [ sec ] とし，時間増分値を 2.0 [sec] としていますので，14400ステップです。