連続境界条件(断熱境界条件):領域左端( X = 0.00 ),上端( Y = 0.05 ),下端( Y = 0.00 )
熱伝達境界条件:右端( X = 0.05 ) 外部流体温度 100 [℃] 熱伝達率 760.0 [ W / m2℃ ]
物性値:熱伝導率:76.0 [ W / m℃ ] 比熱:462.0 [ J / kg℃ ],密度:7870.0 [ kg / m3 ]
図 1 に示すような,初期温度が 20 [℃] 一様である Y 方向に無限に長い平板を考えます。
周囲には温度 100 [℃] の流体があり,板と流体との境界では熱伝達が行われるものとします。
1 分後の温度分布を計算し,理論解と比較します。
なおモデルは対称性を利用して,1/4 モデルとします。
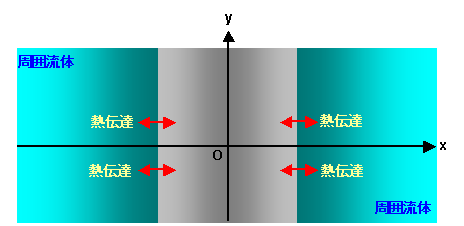
図 1 解析モデル
本例題の場合,解析モデルが原点に関して対称であるので,計算モデルは x = 0 および y = 0 の
境界に対称境界条件を設定することで 1/4 モデルに簡略化することができます。
解析モデルと解析条件を図 2 に示します。
本来は熱量のやり取りが連続している部分を省略するので,対称条件は物理量の連続を補償する性格をもちます。
そのため,ここでは連続条件とあえて表現しています。
この条件を解析モデルの右端以外の境界に設定します。
具体的には,熱流速 q = 0 という条件が設定されます。
有限要素法では,この条件はデフォルトで自動的に設定されるため,
実際にはユーザーが特別に設定する必要がない場合がほとんどです。
つまり、この問題では x = 0 ,y = 0,y = 0.05 の境界に熱量のやり取りがプラスマイナス 0 という連続条件と,
x = 0.10 の境界に周囲流体からの熱伝達による(加熱あるいは冷却),
熱伝達境界条件を設定すればよいことがわかります。
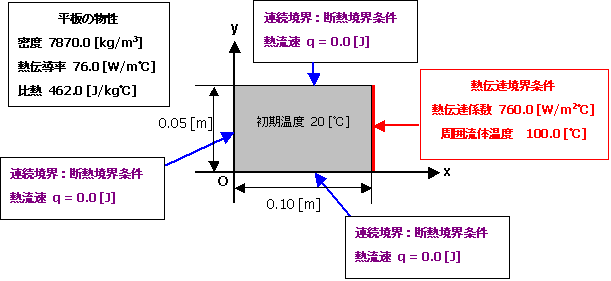
図 2 解析モデル
温度分布グラフ
■平板内の温度
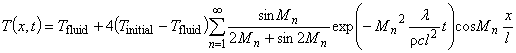
ここで,
Tfluid [℃] :流体温度
Tinitial [℃] :無限板の初期温度
l [m]:無限板の x 方向の長さ
λ [ W/m℃] :無限板の熱伝導率
ρ [ kg/m3 ]:無限板の密度
c [ J/kg℃ ] :無限板の比熱です。
熱伝達率を α [ W / m2℃ ] とすると,ビオー数 B が次式で定義されます。
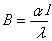
ビオー数に応じて Mn が決定されますが,その値は文献に掲載されています。
参考にした文献には n = 5 までの値が掲載されており,級数展開は n = 5として理論解を計算しました。
なお本例題では B = 1.0 であり,文献より Mn = 12.6453 と読み取ることができます。
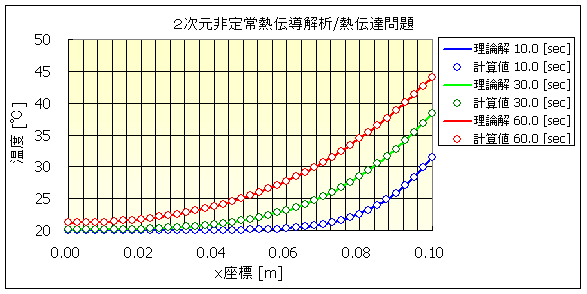
図 3 X [m] における温度分布
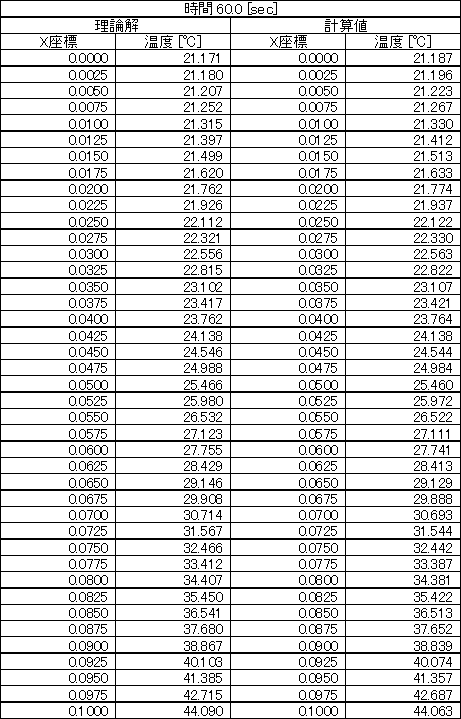
表1 10[sec]における温度分布の理論解と計算値
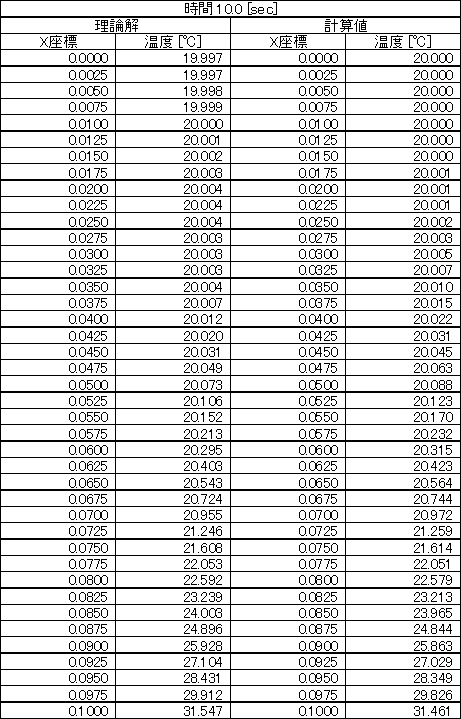
表2 30[sec]における温度分布の理論解と計算値
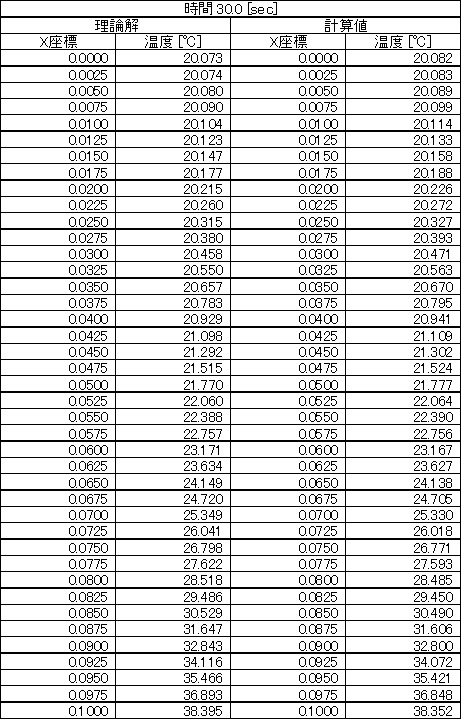
表3 60[sec]における温度分布の理論解と計算値