例題８　平板の非定常熱伝導解析（温度拘束問題）
出典：矢川元基，宮崎則幸：「FEM+BEM=10 有限要素法による熱応力・クリープ・熱伝導解析」，サイエンス社，pp.17〜19（1985）
２次元／非定常／線形／完全陰解法／問題　節点数：451　要素数：800　タイムステップ：0.01 [sec]
境界条件
領域上端（Y=0.05）下端（Y=0.00）：連続境界条件＝断熱境界条件
領域左端（X=0.00）右端（X=0.05）：温度 0.0 [℃]

物性値：熱伝導率：398.0 [ W / m℃ ]　比熱：386.0 [ J / kg℃ ]，密度：8880.0 [ kg / m3 ]

寸法：L1 = 0.10 [m]　L2 = 0.05 [mm]
解析モデル　（フルモデル ）

図 1 に示すような，初期温度が 100 [℃] 一様である平板を考えます。
この平板の左端と右端が時刻 0.0 [sec] より 0.0 [℃] に拘束された場合の平板の温度を計算します。
計算は，時刻 0.0 [sec] から 10.0 [sec] まで完全陰解法により計算し，理論解と比較します。

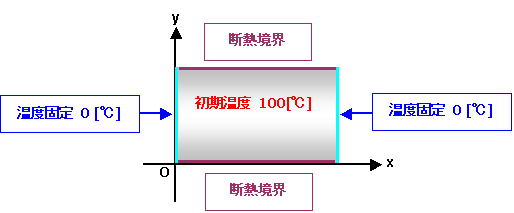
図 1　解析モデル

　

　

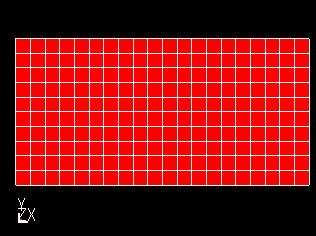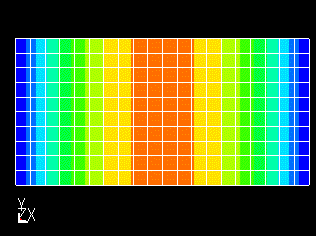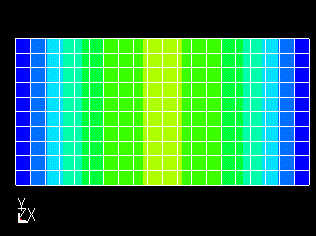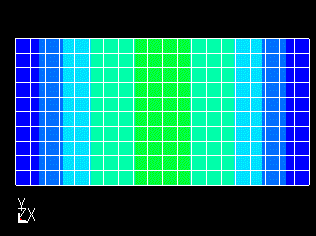
図２　解析モデル

計算結果　温度分布

図 2-1　温度分布 自作コード

図 2-2 LS-DYNA による計算結果

LS-DYNAに関する解析技術のご相談はこちらへ：ランスモア

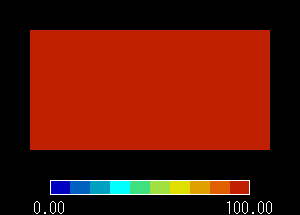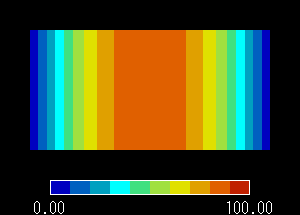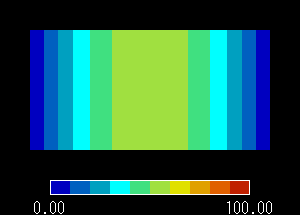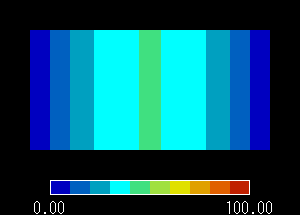
温度分布グラフ

本例題は，x 方向にのみ温度分布が変化する 1 次元問題です．本例題の解析解（*）は次の式で与えられます．

■平板内の温度


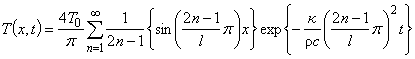
T0 [℃] （固定温度）
λ [W/m℃] （熱伝導率）
c [J/kg℃]（比熱）
ρ [ kg / m3 ] （密度）
l [ m ] （ x 方向の長さ）
t [ m ] （ 時刻 ）
　

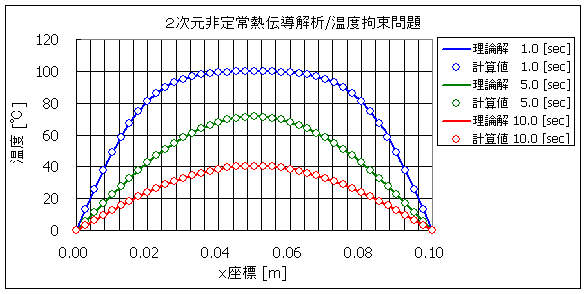
図３　X[m] における温度分布

数値データ
表1-3に数値データを示します。

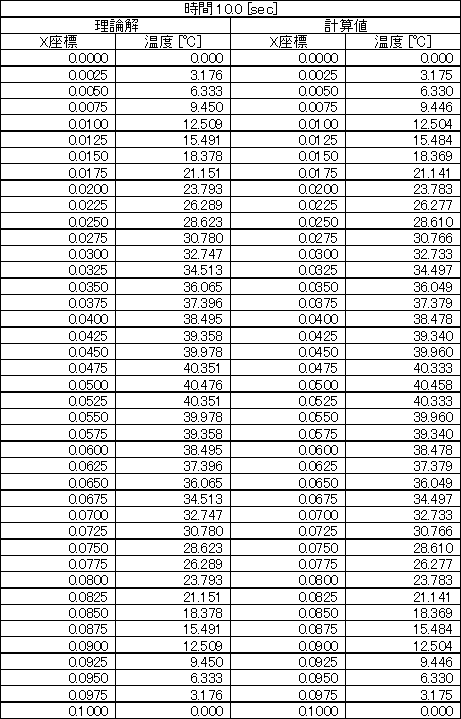
表１　1.0[sec]における温度分布の理論解と計算値

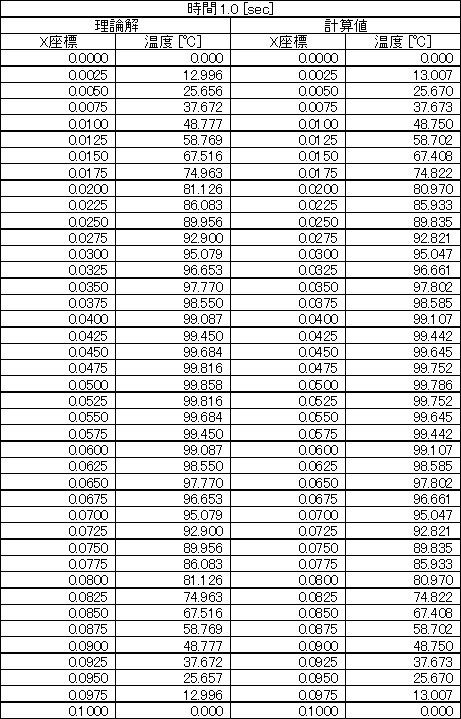
表２　5.0[sec]における温度分布の理論解と計算値

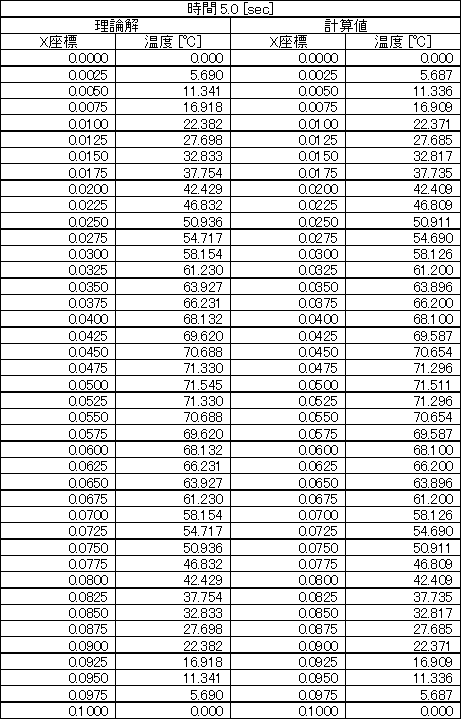
表３　10.0[sec]における温度分布の理論解と計算値