例題７　厚肉円筒の軸対称定常熱伝導解析（熱伝達問題）

例題７　厚肉円筒の軸対称定常熱伝導解析（熱伝達問題）
出典：鷲津，宮元，山田，山本，川井編：「有限要素法ハンドブックⅡ」，培風館，p.457-459
軸対称／定常／線形／問題　節点数：231　要素数：400（三角形1次要素）
境界条件 ○内壁熱伝達境界条件　内部流体温度 60 [℃]　熱伝達率 0.048 [ W / mm²℃] ○外壁熱伝達境界条件　外部流体温度 20 [℃]　熱伝達率 0.015 [ W / mm²℃]
物性値領域１の熱伝導率 λ ：0.025 [ W / mm℃ ]
寸法 r₁ ： 50 [mm]　r₂ ： 150 [mm]　h：50 [mm]
2010年1月26日読者の方からのご指摘で以下に示す円筒の外壁温度の式中に符号の誤りがあることがわかりましたので訂正いたしました。ご覧いただいている皆様には大変ご迷惑をおかけしました。すみません。またご指摘いただいた方に感謝いたします。ありがとうございます。
解析モデル　（軸対称モデル）
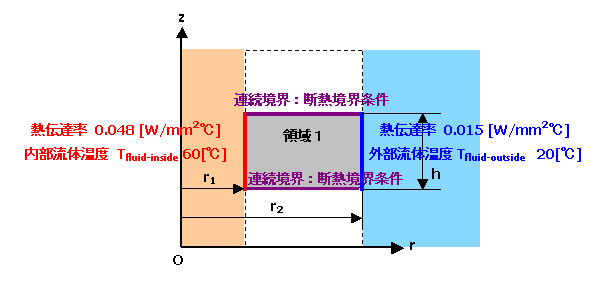
図 1 解析モデル
計算結果　温度分布
図 2-1 温度分布　自作コード　図 2-2　LS-DYNA による計算結果 LS-DYNAに関する解析技術のご相談はこちらへ：ランスモア
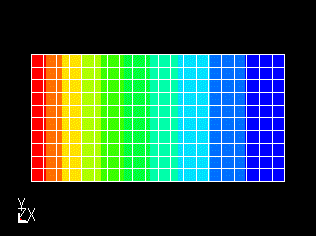
温度分布グラフ
本問題においては，半径方向 r [mm] の温度分布の理論解を次の式により求めることができます。
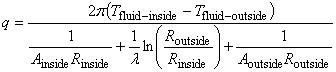
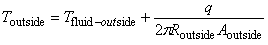
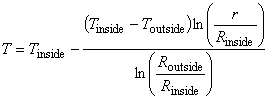
■領域 1 を通過する熱量 q ■円筒の内壁温度 T_inside ■円筒の外壁温度 T_outside ■円筒内部の温度 T q ：熱流速 λ ：熱伝導率 T_fluid-inside ：内部流体温度 A_inside：内部流体と領域 1 との間の熱伝達率 T_outside：外部流体温度 A_outside：外部流体と領域 1 との間の熱伝達率 R_inside：円筒の内径 R_outside：円筒の外径

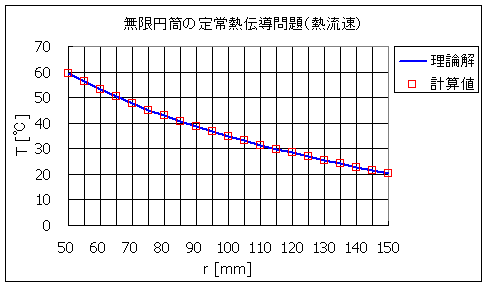
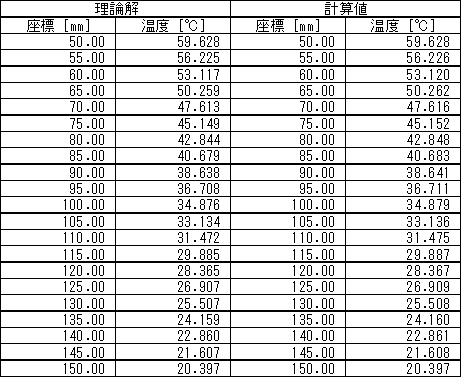
図 3 半径 r における温度分布
数値データ
表1に数値データを示します。
表 1 温度分布の理論解と計算値