
 Math and Physics
Math and Physics
ホーム > 数学と物理の予備知識 TOP > 数学と物理の予備知識 No.009
関数形が既知で変数が 1 つである 1 変数関数の場合における,Newton-Raphson法のイメージは 2 章で理解できたと思います。
ここでは収束と初期値の関係を簡単なイメージで捉えてみます。
図 1 に簡単な関数の模式図を示します。
初期値が,S0 の場合に解 S を求める場合は,2 章で学んだ方法により収束解を得ることができそうです。
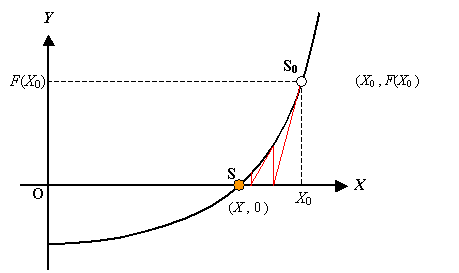
図 1 初期値と解の関係 1
図 2 に初期値が異なるケースの収束プロセスを示します。
この場合,反復計算の 1 回目に得られる近似解は,真の解を超えてしまいますが,2 回目の反復計算からは図 1 で示した過程と同様の収束計算に移行し収束解を得ることができそうです。
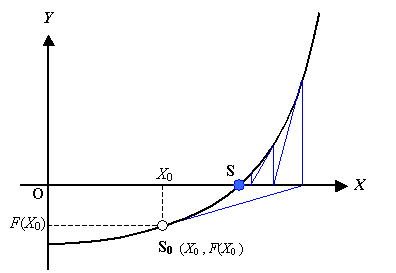
図 2 初期値と解の関係 2
図 3 に初期値が真の解から離れている場合のケースを示します。
このような場合は,近くの解を収束解と判断してしまうため,求めたい解を得ることができない例です。
参考書等で,「初期値を解の十分近くに取れば・・・」というくだりはこのことを意味します。
現実には真解がどこにあるか事前には分からないので,毎回必ず初期値を解の十分近くに取ることはできません。
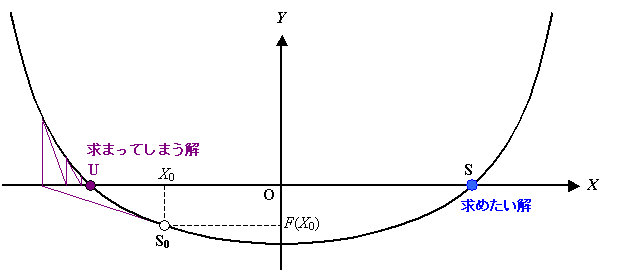
図 3 初期値と解の関係 3
図 4 に収束解が得られない例を示します。
関数の変曲点では,勾配が 0 となるのでこの関数の場合には,過渡解すら見出すことができません。
このような場合の対策は,まずは初期値を少しずつ移動してみることです。
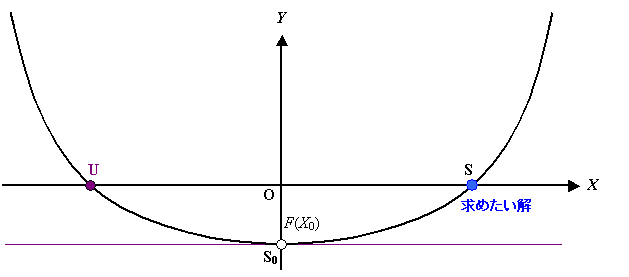
図 4 初期値と解の関係 4
図 5 は収束解を得ることが困難な例です。
初期値が真解に近い場合は,すぐに収束解を得られそうですが,図のように初期値が真解より離れるといつまでたっても真解に近づくことができない場合があります。
このような場合も,初期値を少しずつ移動してみることを検討する必要があります。
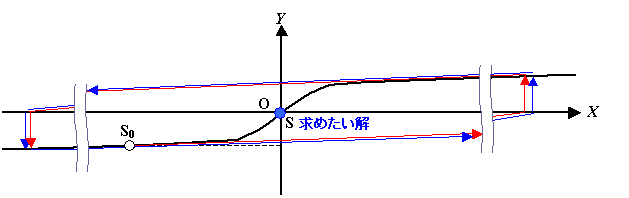
図 5 初期値と解の関係 5