有限要素法では,解析に使用する要素を決定すると,離散化された有限要素式を求めることができます。
逆にこのことは,使用する要素ごとに離散化して得られる有限要素式が異なるということを意味します。
ここでは,有限要素法で最も簡単な要素である三角形 1 次要素について説明します。
三角形 1 次要素は,有限要素の中でもっともシンプルな要素です。
しかしながら,この要素は他の要素に比べて大きな特徴があります。
それは領域積分において積分公式を使うことが可能であるため,数値積分を必要としないということと,
任意形状に対する自動要素分割アルゴリズムが確立されているということです。
ほとんどの教科書では三角形 1 次要素を中心に解説が行われています。
まず,図1に三角形 1 次要素を示します。
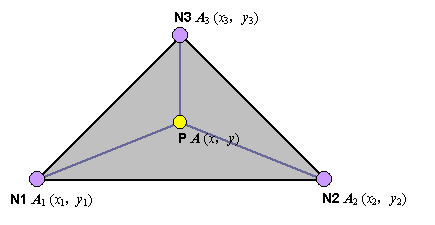
図1 三角形1次要素の概要
そして,要素内の任意点 P におけるベクトルポテンシャル A を,未知係数 r , s , t を用いて 次のように 1 次式で近似します。
1 次式で近似していますので,各節点(頂点)間において節点ポテンシャル値は線形(直線状)に変化します。
例えば,節点 1 でのポテンシャル A1 の影響は節点 1 で 100 % であり, 節点 2 および 3 で 0 % となるように線形に変化します。
節点 1 でのポテンシャル A1 の影響は,辺 2 - 3 上でも 0 %です。
節点 2 でのポテンシャル A2 は節点 2 上ではその影響が 100 % であり, 節点 1 と 3 では 0 % となります.また辺 1 - 3 上でも 0 % です。
このように三角形 1 次要素は,要素内でのポテンシャル分布を 1 次式で近似します。
そのため,磁性体近傍のような場の変化が急激なところでは,要素分割を細かくしないと 解析精度が落ちてしまいます。要素サイズより小さな現象は,解像度が足りなくて解析結果に反映されないからです。
したがって,場に対して粗い分割であると現象を拾いきれない可能性が出てきます。 よくいう精度云々という話はここから来ています。
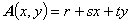
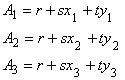
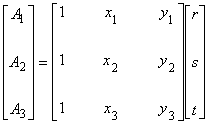
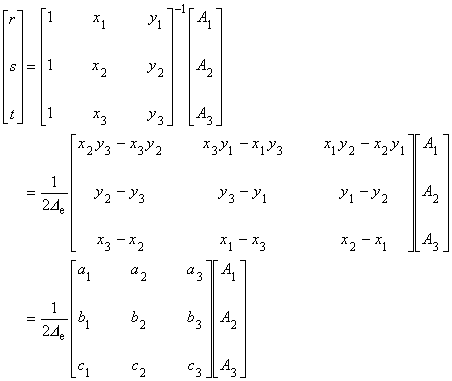
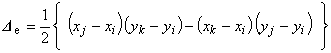
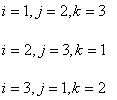
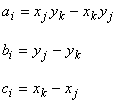
したがって,未知係数 r , s , t は次のように求まることがわかります。
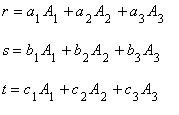
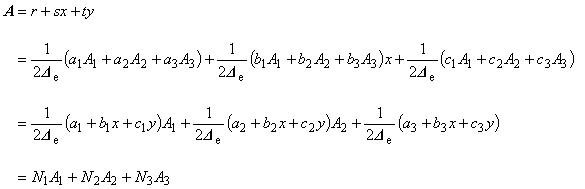
ここで,
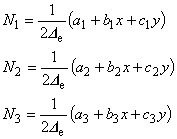
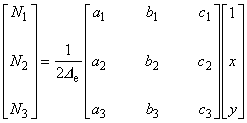
以上より,要素内の任意点におけるポテンシャル A は, 次のように表現することができることがわかりました。
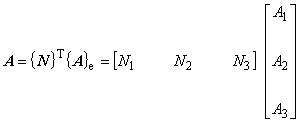
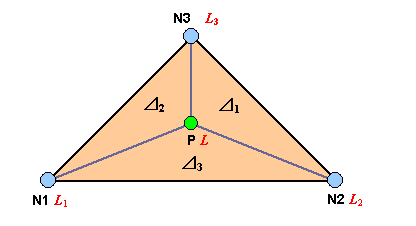
図2 三角形 1 次要素と面積座標
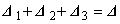
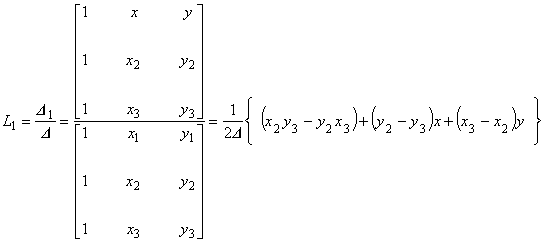
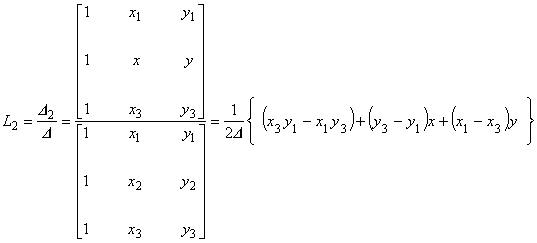
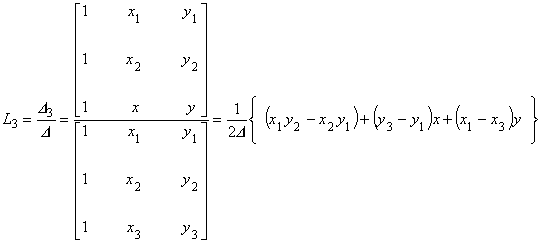
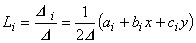
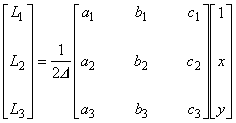
式(5.11)と式(5.15)は,形状関数{L}が要素の内挿関数{N}と一対一の対応にあることを示しています。 したがって,次の式が成り立つことは明らかです。
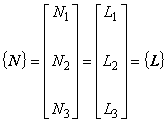
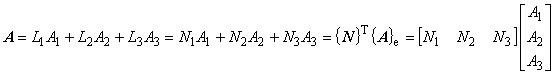
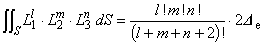
1つ目は静磁場項[S]を三角形 1 次要素を用いて離散化する例であり,2 つ目は駆動電流密度項{J}, 3つ目は渦電流の容量行列[E]に対する適用例です。
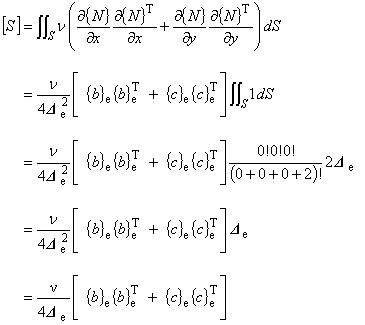
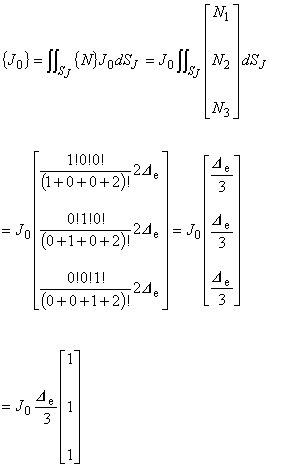
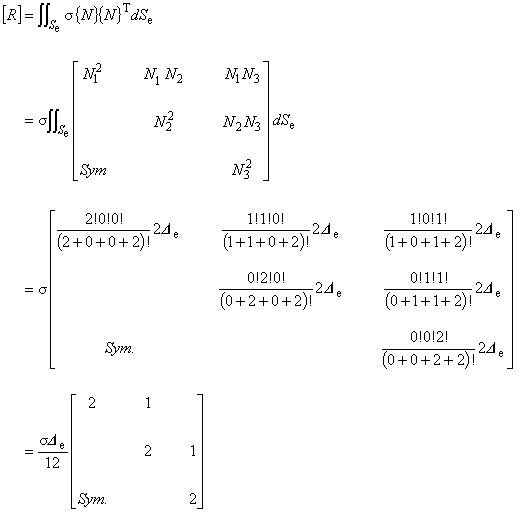
三角形 1 次要素は,有限要素法で用いられる要素としては最も易しい要素です。
しかしながら,要素分割アルゴリズムが普及していることと,積分に面積積分の公式が使用でき,
数値積分を必要としないなどの大きなアドバンテージを持っており,多くの参考書で取上げられています。
1 次要素ですが,要素分割を細かくすることで,解析精度を維持するよう対応します。
磁場のように解分布が指数関数的に変化するような問題では,要素数が増える懸念はありますが,
最近は計算機のパワーが向上しているので静解析などでは10万要素以上の計算でも容易に解くことができます。
ただやみくもにメッシュを作る必要はなく,解の精度は目的が達成できる程度で十分です。
解析の開発者や研究者以外は,解析は問題解決のツールであって,問題が解決されることを優先しなくてはなりません。



