まず,三角形要素の頂点 1 と 2 を結んでできるベクトルを P ,頂点 1 と 3 を結んでできるベクトルを Q と すると成分は次のようになります。
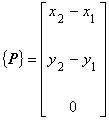
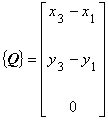
(6.1)
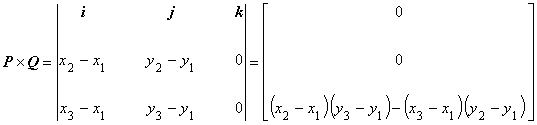
(6.2)
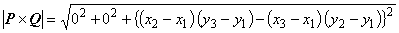
(6.3)
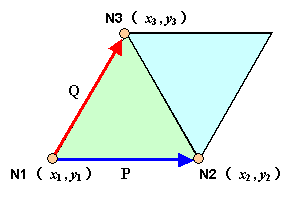
図1 ベクトルの外積と三角形要素の面積
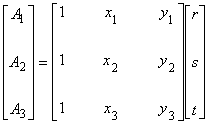
(5.3)
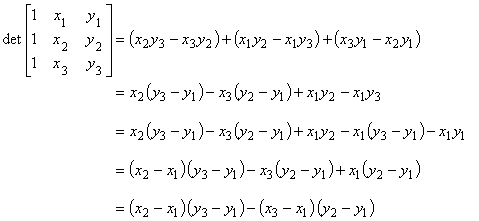
(6.4)
すなわち,
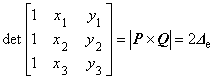
(6.5)
すなわち,
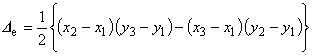
(6.6)
| 2 次元磁場解析 No.6 / ガラーキン法 / 三角形要素の面積 | |
| 三角形要素の内挿関数を導出する際に三角形要素の面積⊿が現われますが,これは次のようにして導かれます。 まず,三角形要素の頂点 1 と 2 を結んでできるベクトルを P ,頂点 1 と 3 を結んでできるベクトルを Q と すると成分は次のようになります。 |
|
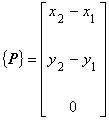 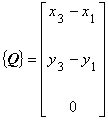
|
(6.1)
|
| このとき,外積 P × Q は次のように計算されます。 | |
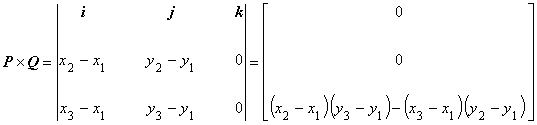 |
(6.2)
|
| この外積の大きさは, | |
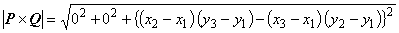 |
(6.3)
|
| これは,下の図1に示すような三角形要素の 2 倍の平行四辺形の面積表します。 |
|
|
図1 ベクトルの外積と三角形要素の面積 |
|
| 一方,式(5.3) | |
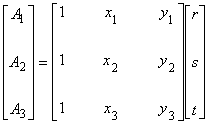 |
(5.3)
|
| のマトリックスの行列式は次のようにして計算されます。 このとき,途中の式変形に注意してください。 | |
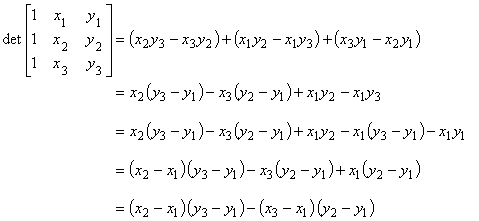 |
(6.4)
|
| したがって,これは式(5.5)と等しいことがわかります。 すなわち, |
|
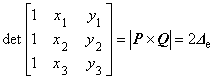 |
(6.5)
|
| 行列式は三角形要素の面積の 2 倍を表していることがわかります。 すなわち, |
|
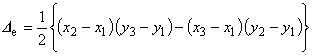 |
(6.6)
|
| であることが示されました。 | |