2 次元磁場解析 No.3 / ガラーキン法 gradφ項の離散化

図 2 に示すように，導体あるいは磁性体に鎖交する磁束が変化すると， 磁束に垂直な平面に渦電流が流れることはよく知られた事実です．
例えば，交流電流のような磁場の変動や導体が磁場中を移動する場合がこれに相当します．
渦電流は「磁束の変化を妨げるような方向」に反作用磁場を発生させます．
また一般の機器においては渦電流による発熱も問題となってきます．
したがって，渦電流の影響を評価することは磁場解析の中で特に重要なテーマですが，解析の難易度も高くなります．
ここでは，渦電流の反作用磁場の影響を考慮する方法を説明するにとどめます．

２次元場の磁場解析の支配方程式は式（2.2）のようになります。

（2.2）
左辺第 3 項に対するガラーキン法の適用について考えます。
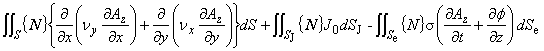
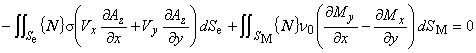
２次元場では，駆動電流は z 方向成分のみ有するので，渦電流も z 方向成分のみを有します。
第 3 項の渦電流密度項は次のように与えられることをすでに示しました。
（3.1）
ここで，渦電流は磁性体に鎖交する磁場の時間変化に伴い，磁性体内部に誘起する電流であるので， 磁性体や導体に対して外部から電荷が供給されるわけではありません。
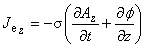
したがって，渦電流が流れる磁性体または導体には電荷の蓄積がおこらないので， 同一導体について電荷は渦電流が流れる前と後で変わらず，つまり次の電荷保存式が成り立つと考えられます。
（3.2）
積分形の表現に直してみます。
（3.3）
２次元場では，ベクトルポテンシャル A や駆動電流密度 J がそうであるように， 渦電流密度 Je [ A/m2 ] は z 方向成分のみを有し， またその z 方向分布は一定（不変）であると仮定しています。
（3.4）
（3.5）
一方２次元場では，スカラーポテンシャルφ（電位）は z 方向にのみ変化し， x , y 方向については変化しないことを仮定します。 もし，x,y 方向について変化してしまうと，式(3.4)より次式で表されるように 渦電流密度 Je が x , y 成分を有することになります。
（3.6）
このことは，２次元場の仮定に矛盾するため，スカラーポテンシャルは z 方向のみ変化するものとして扱われます。
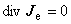
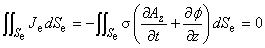
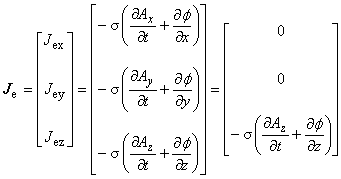
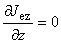
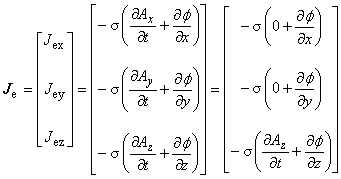
したがって，２次元場では次の設定が導かれます。
スカラーポテンシャル（電位）がz方向にのみ変化し，x,y方向には変化しない
---> 渦電流が流れる磁性体または導体について，z 断面である xy 平面では， 同一の磁性体ないし導体であれば至るところで電位が等しい。（２次元場において）
---> 同一導体の xy 平面上では至るところでスカラーポテンシャル（電位）の z 方向の勾配が等しい。
すなわち
（3.7）
のようになります。
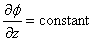
以上で，スカラーポテンシャルの性格がわかったので，式(3.3)にもどって考えてみます。
（3.3）
まず式（3.3）を積分項ごとに分離します。
（3.8）
次に grad φ 項を移項して整理します。
（3.9）
先に述べたように２次元場では，スカラーポテンシャルの勾配は一定値であり， 解析領域の xy 平面上では一定値となり積分対象の外側へ出されます。
（3.10）
gradφについて解くと，
（3.11）
となります。
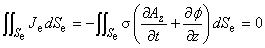
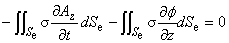
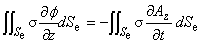
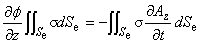
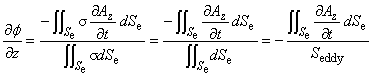
ここで，Seddy は，渦電流が流れる導体の全面積を表します。
式（3.11）は，スカラーポテンシャルの勾配が， 渦電流領域におけるベクトルポテンシャルの時間変化の領域平均を表すことを示しています。
つづいて，式（3.11）を式（3.1）に代入すると次式を得ます。
（3.12）
この項にガラーキン法を適用すると次式のようになります。
（3.13）
ここで，要素内の任意点でのベクトルポテンシャル A を， 要素の内挿関数 {N} と節点のベクトルポテンシャル {A}e によって次式のように近似します。
（3.14）
このとき式（4.13）は，次式のように表すことが可能です。
（3.15）
右辺第２項のスカラーポテンシャルの勾配を表す項について考えてみます。
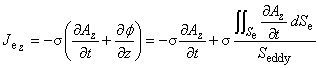
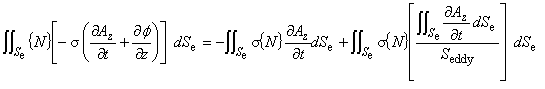
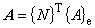
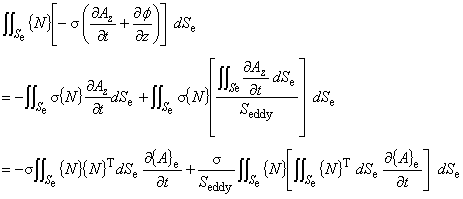
被積分関数の中にある積分から考えます。途中の積分は面積積分の公式を使用します。
また，時間微分項は１階の後退差分近似として扱います。
（3.16）
式（3.16）のこの先の取り扱いについて簡単な例を参考にして説明します。
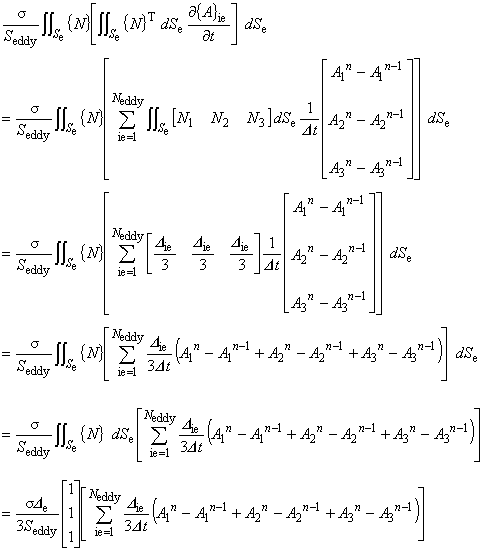
下図に示すようなメッシュを考えます。ハンドルしている要素番号を 2 とします。

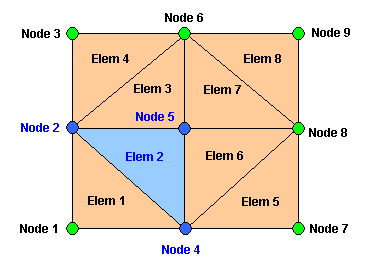
図　メッシュ アクティブエレメントは 2 ，構成節点は 4--->5--->2

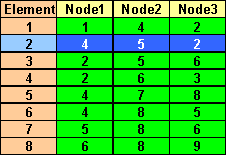
このメッシュモデルの要素番号−構成節点番号のコネクティビティを示します。

要素番号と構成節点番号のコネクティビティ

要素番号 2 をアクティブに考え，式（3.16）を具体的に展開してみます。
（3.17）
これを節点ポテンシャルについて整理すると，次式のようになります。
（3.18）
ただし，
（3.19）
すなわちマトリックス部分は，同一導体の渦電流要素を構成する要素の面積で構成されていることがわかります。
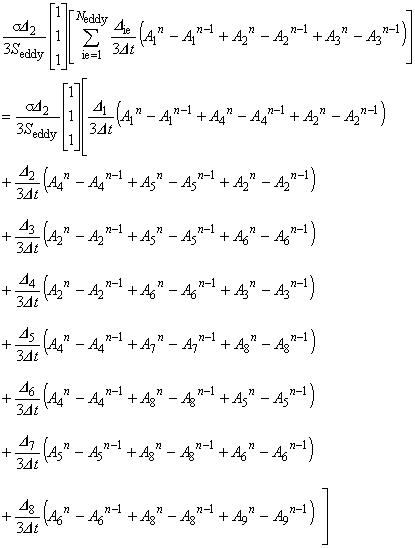
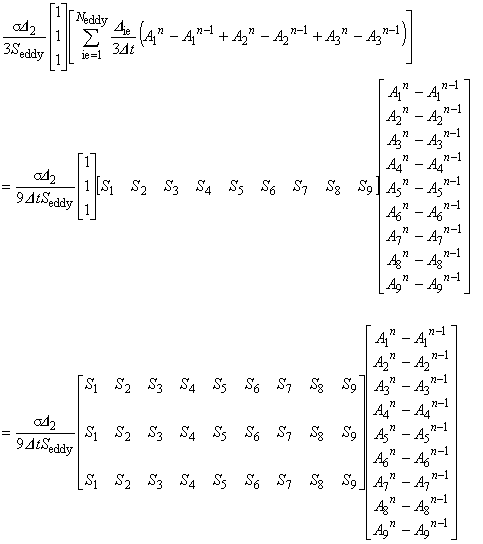
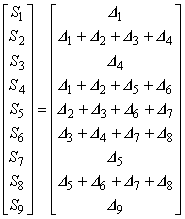
この例でわかるように，同一導体の渦電流要素が増えるに従って， マトリックスの 1 行あたりの非零要素数が増加します。 極端な場合，解析領域すべてが渦電流要素だと全節点数と非零要素数が等しくなり， 連立一次方程式を解くためのメモリーを圧迫します。 したがって，この手法には記憶容量という面で不利です。

以上より，式（4.15）の一般形は次のようになります。

（3.20）

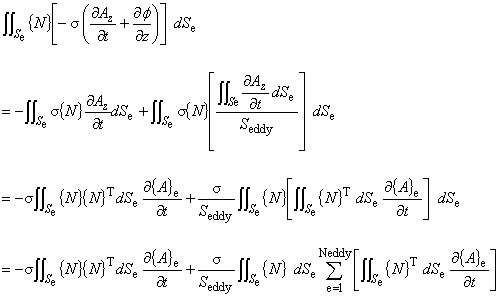
ここで取り上げた渦電流の取り扱い手法に関する参考文献を紹介します。
1）中田高義，河瀬順洋：有限要素法による積層鉄心接合部の磁界解析，昭和58年電気学会論文集Ｂ45　P.358
2）中田高義，高橋則雄，河瀬順洋：うず電流解析における電界（gradφ）の物理的意味の考察， 電気学会情報処理研究会資料 IP-80-49（1980）
3）加川幸雄，山淵龍夫，村井忠邦，土屋隆生：FEMプログラム選２ 磁界・電磁波，森北出版，第 3 章
4）加川幸雄，榎園正人，武田毅：電気・電子境界要素法，森北出版，第6章，7章など