渦電流の時間依存項である式 (5.2) の左辺第 8 項は,次のように変形できます。
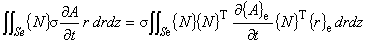
(6.1e)
目的はベクトルポテンシャルの項を積分対象から除外できる形に変形することです。
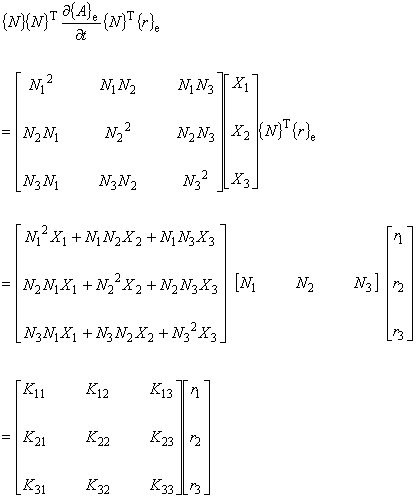
(6.2e)
(6.3e)
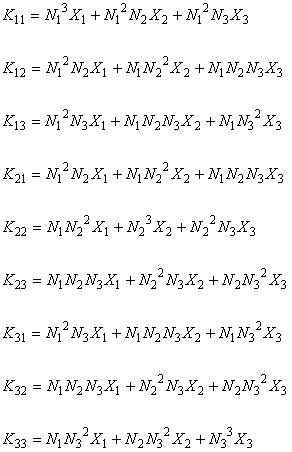
(6.4e)
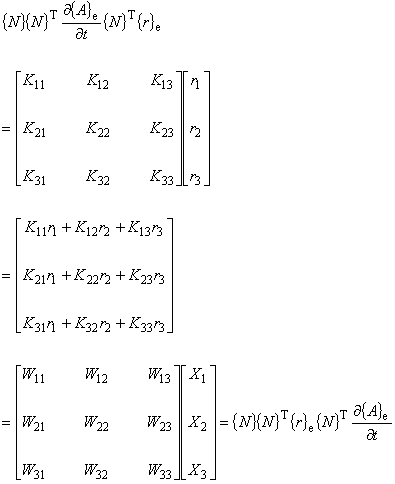
(6.5e)
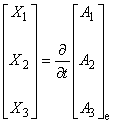
このようにしてベクトルポテンシャルの時間依存項を最後にもってくることで, 積分対象から除外することが可能になります。
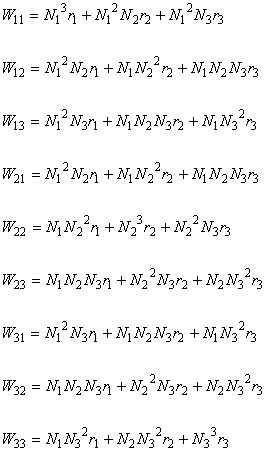
(6.6e)
(面積積分の公式)
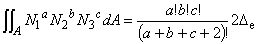
(6.7e)
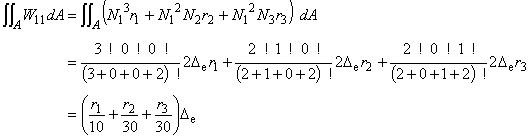
(6.8e)
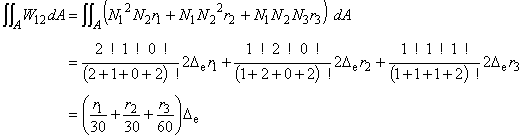
(6.9e)
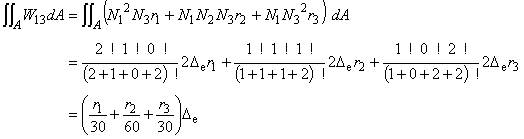
(6.10e)
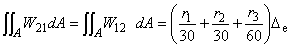
(6.11e)
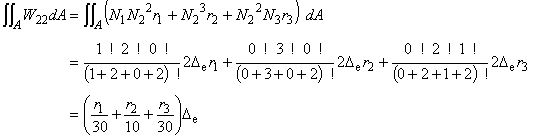
(6.12e)
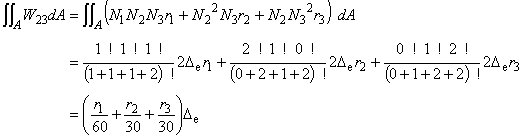
(6.13e)
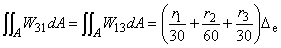
(6.14e)
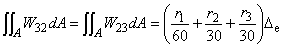
(6.15e)
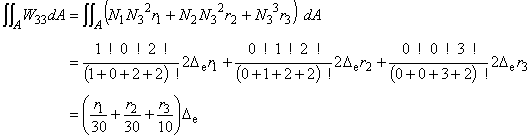
(6.16e)
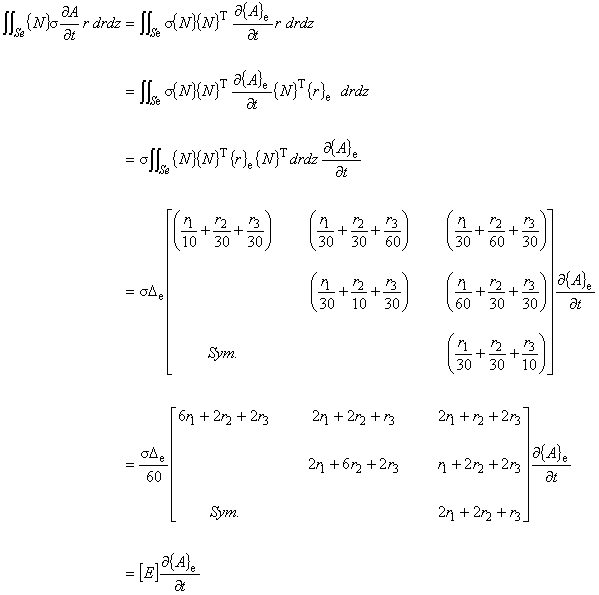
(6.17e)
E マトリックスの成分を見て下さい。平均化の分だけ差があることがわかると思います。
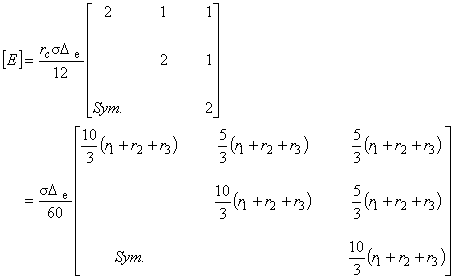
(6.18e)



