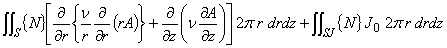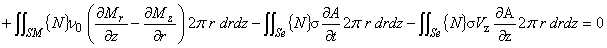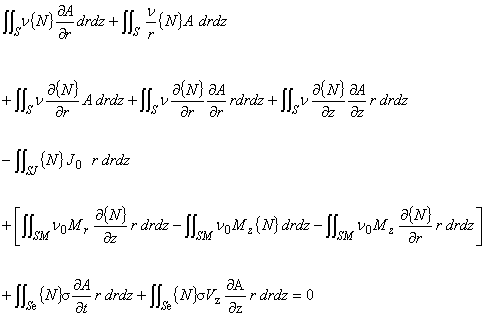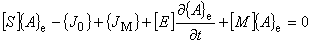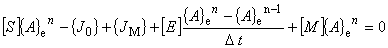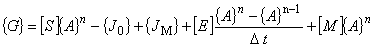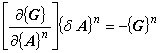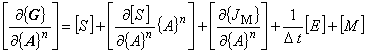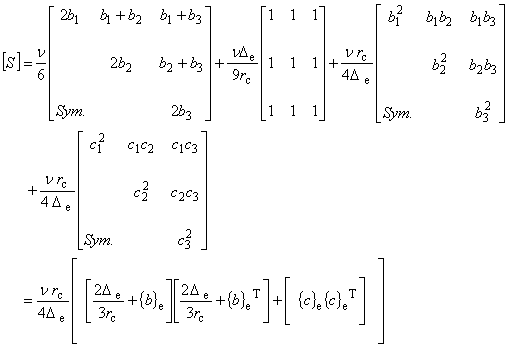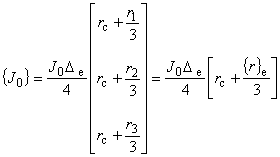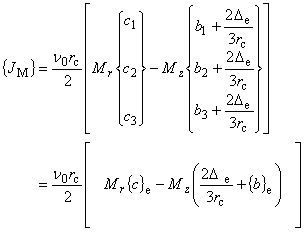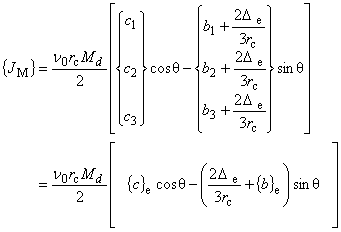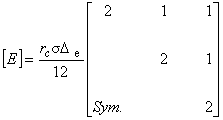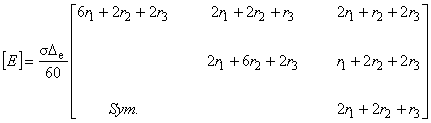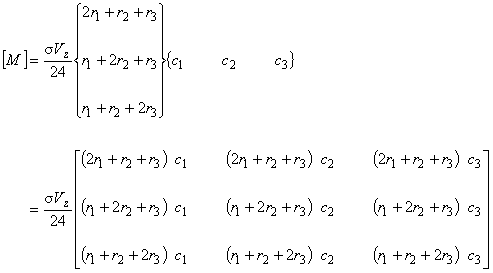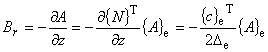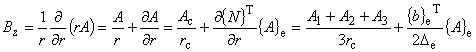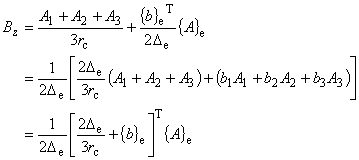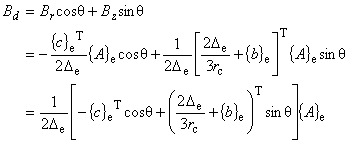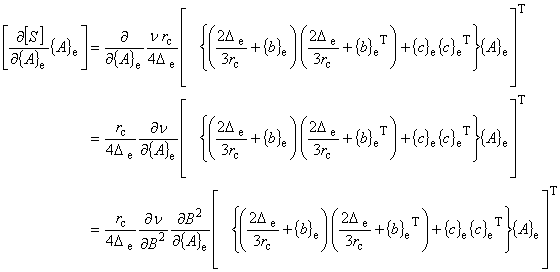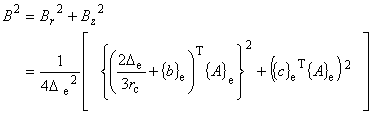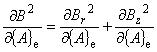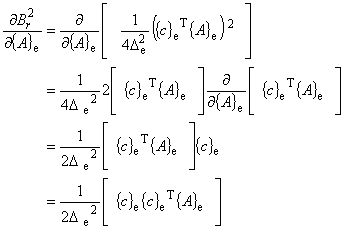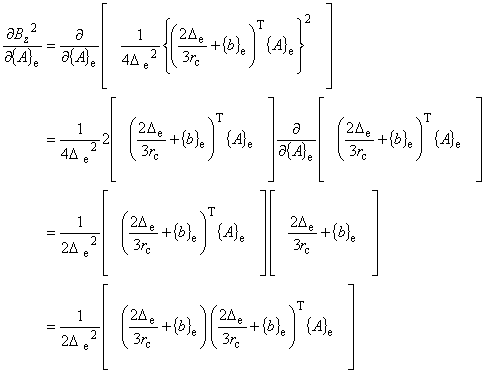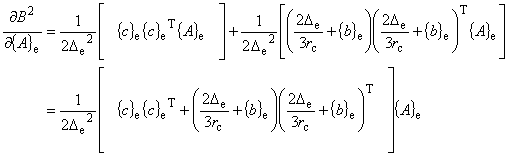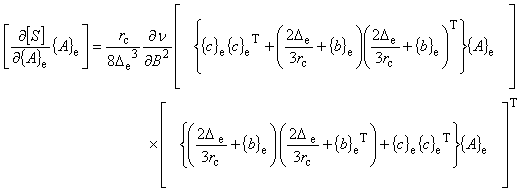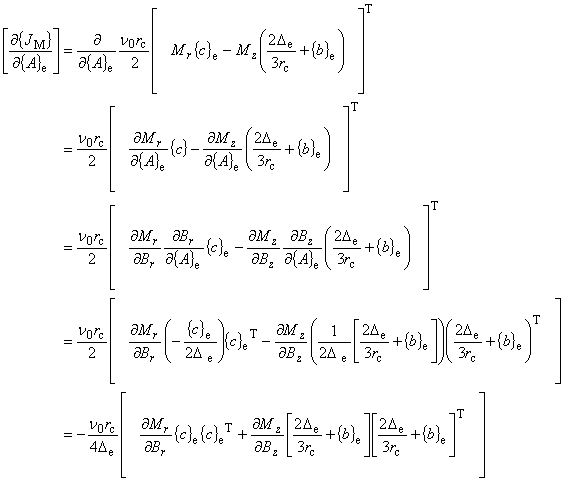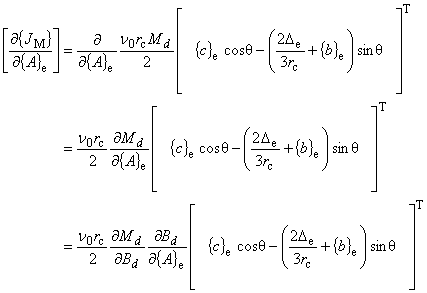軸対称磁場解析 7 / 有限要素式

軸対称磁場解析 7 / Newton-Raphson法に対応した有限要素式
一般に，磁界問題は磁性体の磁気特性が非線形性を有しているため，磁気飽和や永久磁石の非線形磁化特性を考慮する場合には，反復解法によらねば有限要素式の解を得ることができません。ここでは，反復解法として Newton-Raphson 法を採用し，必要なコンポーネントをまとめてみます。軸対称磁場問題の支配方程式にガラーキン法を適用した式は次のように表されました。
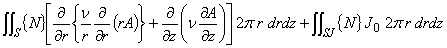
	（1.18）
ガラーキン法を適用した式を弱形式化した式は次のように表されました。
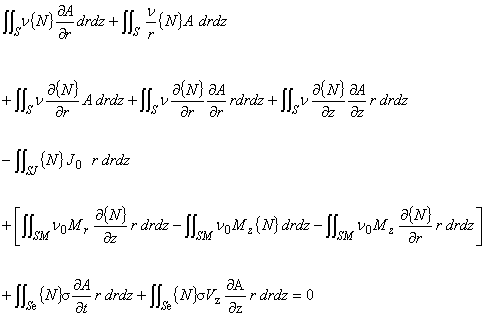	（5.2）
三角形環状 1 次要素を用いて離散化すると，次の有限要素式が得られました。
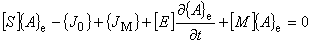	（6.16）
渦電流が関係する時間依存項を一階の後退差分で近似すると次のように変形されました。これは磁場の線形解析用の有限要素式となります。ベクトルポテンシャルの肩の添え字 n は，タイムステップ n を表します。 n-1 は一つ前のタイムステップを表します。解析領域中に駆動電流（励磁電流)が流れるコイルが存在しない場合は，{J₀} が 0 になります。永久磁石や磁化ベクトル M を考慮しない場合は，{J_M} が 0 になります。渦電流を考慮しない場合は，[E] が 0 となり，導体の運動に起因する渦電流を考慮しない場合は [M] が 0 となります。
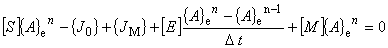	（6.17）
非線形問題の場合 Newton-Raphson 法
磁性体の非線形磁気特性を考慮した解析では，解を得るためには反復解法によって有限要素式を解きます。ここでは，反復解法としてNewton-Raphson 法を採用します。このとき有限要素式を次のように {G} という{A}の関数としておいてみます。
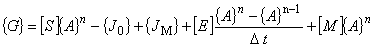	（7.1）
そして，次の非線形方程式を解くことで磁気ベクトルポテンシャル A の増分値 δA を得ます。
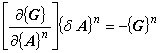	（7.2）
得られた磁気ベクトルポテンシャルの増分値より最新の磁気ベクトルポテンシャルにアップデートします。 Aⁱ⁺¹ = Aⁱ + δA このアップデートを A の変化が収束するまで繰り返すことで，時刻 N におけるベクトルポテンシャルが求まります。
ここで，式(7.2)の左辺の行列を接線係数マトリックスあるいは感度行列などとよびます。この接線係数マトリックスをマトリックスとベクトルのコンポーネントで表すと次のようになります。接線係数マトリックスは，{G} を {A} で偏微分したものです。
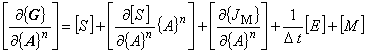	（7.3）
静磁場マトリックス [S] および等価磁化電流密度ベクトル {J_M} は，内部に磁場 B に依存した成分を有しており，B は {A} の関数であるため，偏微分の対象となります。各マトリックスとベクトルをまとめると次のようになります．
静磁場マトリックス [S]
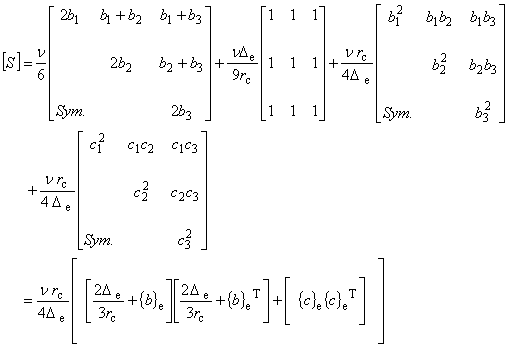	（7.4）
駆動電流密度ベクトル {J₀}
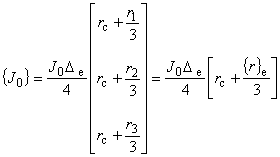	（7.5）
等価磁化電流密度ベクトル {J_M} 直交異方性表示
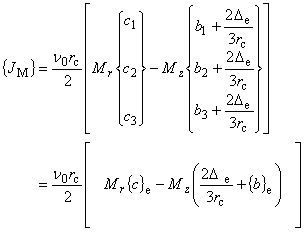	（7.6）
等価磁化電流密度ベクトル {J_M} 任意の磁化方向を考慮した表示
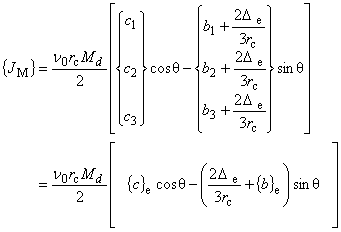	（7.7）
渦電流時間依存項 1 / [E] マトリックス / r を要素の重心座標で近似した表示
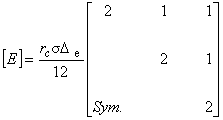	（7.8）
渦電流時間依存項 2 / [E] マトリックス / r を正確な面積積分で評価した表示
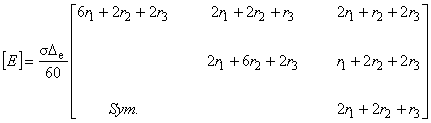	（7.9）
渦電流速度起電力項 / [M] マトリックス /
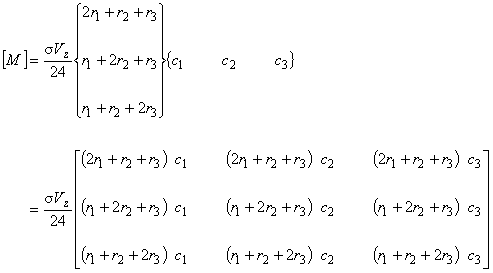	（7.10）
軸対称場の磁場 B [T] の計算
軸対称場では，磁場 B [T] は，三角形環状 1 次要素を使用した場合，次のように表されます。
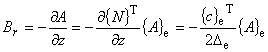	（7.11）
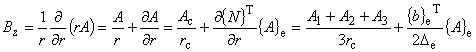	（7.12）
磁場 B の z 方向成分を表す式(7.12)において，左辺第 1 項の分母の r は，要素重心における r 座標で近似するため，分子の磁気ベクトルポテンシャル A も要素重心における値 A_c で近似します。
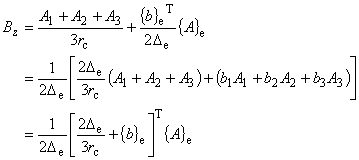	（7.13）
さらに，等価磁化電流密度項で，任意の磁化方向を考慮する場合，磁化 M_d と同じ方向の磁場 B_d を知っておく必要があります。これは次のようにして求めます。
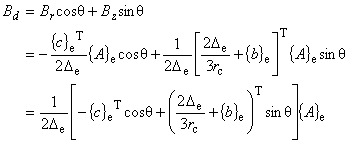	（7.14）
接線係数マトリックス 1 / 静磁場微分項 /
軸対称場における磁場 B が求められたので，非線形項を求めることができます。
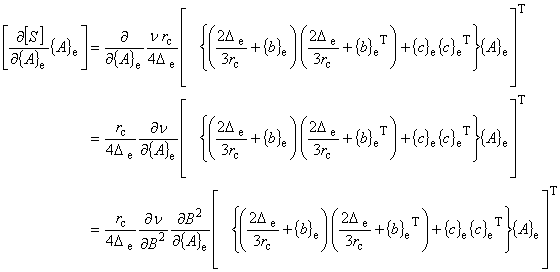	（7.15）
ここで，磁場 B の絶対値は式(7.11)および(7.13)より，
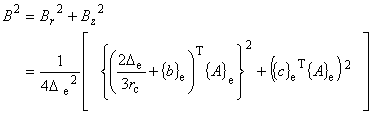	（7.16）
です．したがって，磁気ポテンシャル A による偏微分は次のようにして計算されます。
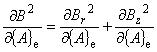	（7.17）
式(7.17)の右辺第 1 項について，
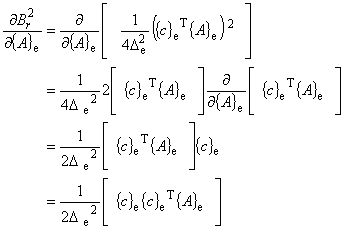	（7.18）
式(7.17)の右辺第 2 項について，
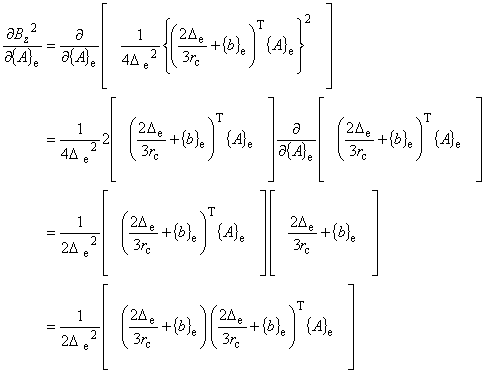	（7.19）
式(7.18)と(7.19)より，磁場 B の 2 乗の偏微分は次のようにして求めることができます。
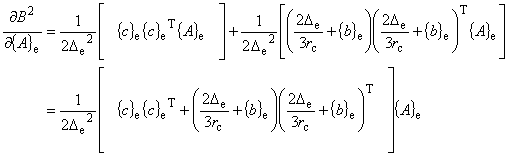	（7.20）
式(7.20)を式(7.15)に代入すれば，静磁場微分項を求めることができます。
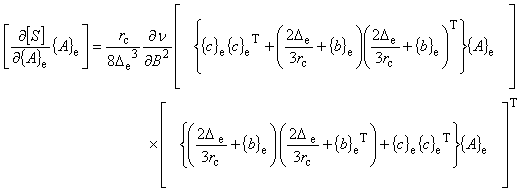	（7.21）
接線係数マトリックス 2 / 等価磁化電流密度微分項 / 直交異方性考慮
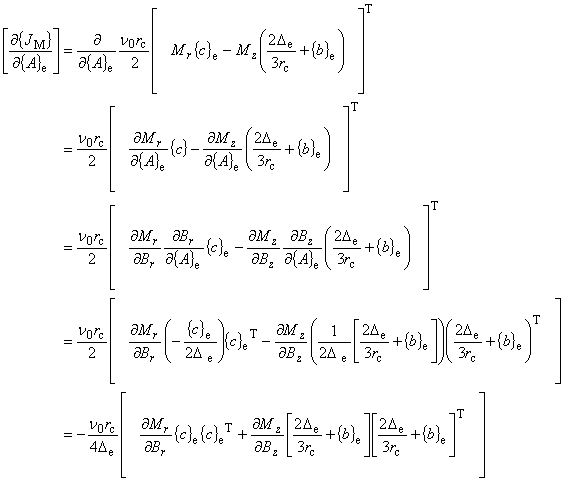	（7.23）
接線係数マトリックス 2 / 等価磁化電流密度微分項 / 任意磁化方向考慮
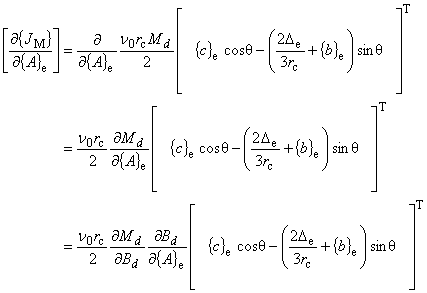	（7.24）
ここで，式(7.14)より，
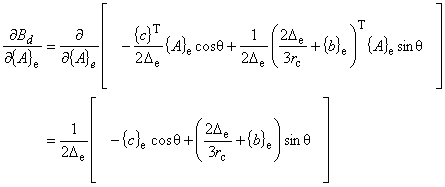	（7.25）
であるので，式(7.25)を式(7.24)に代入すれば，任意の磁化方向を考慮した等価磁化電流密度微分項が，次式のように求まります．
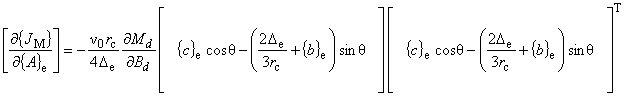	（7.26）
以上で，Newton-Raphson 法による非線形計算で必要となる軸対称磁場解析の有限要素式の成分が明らかになりました。