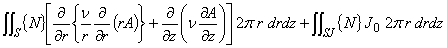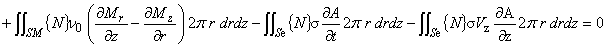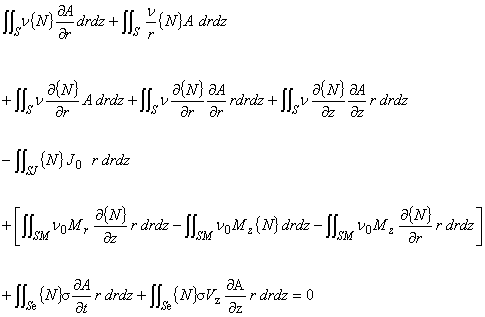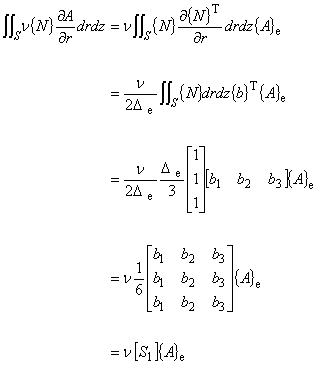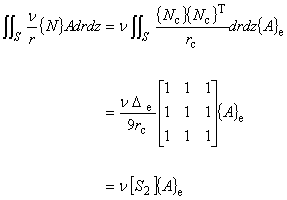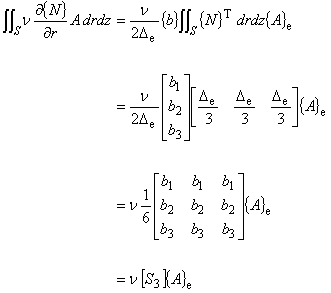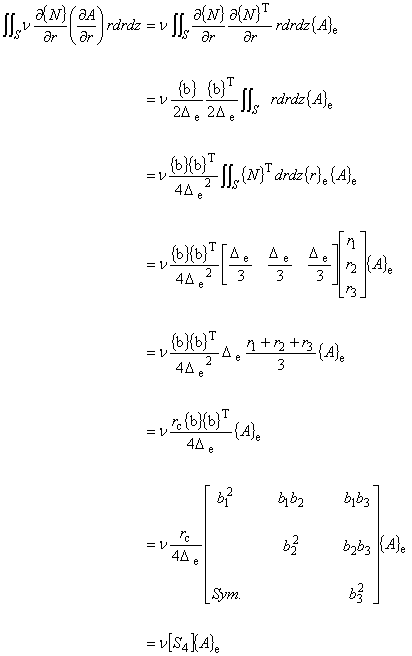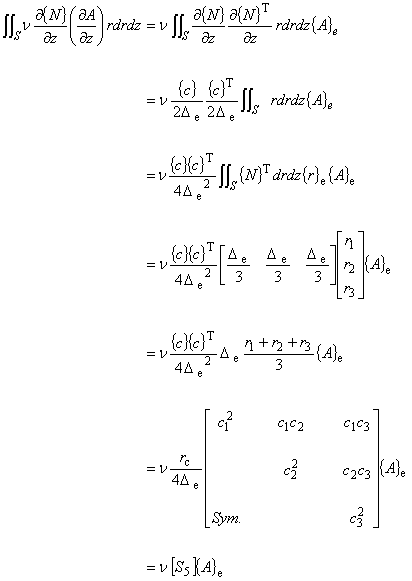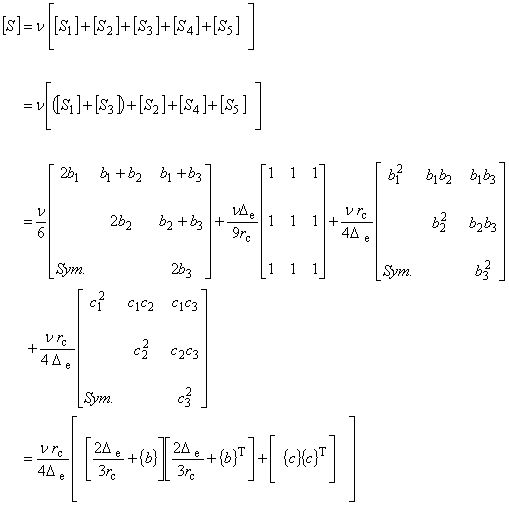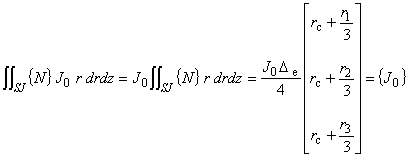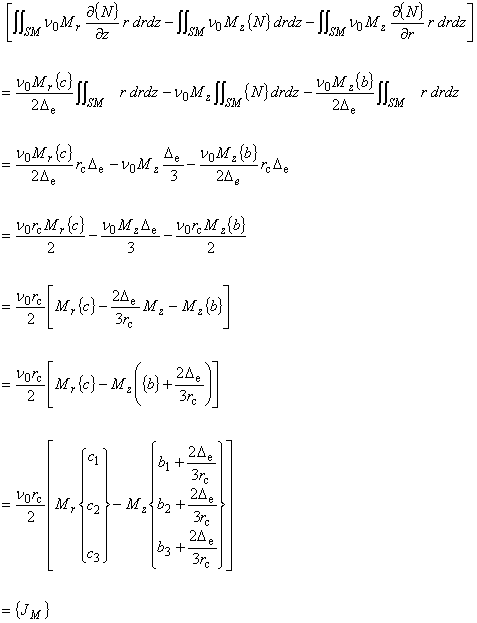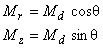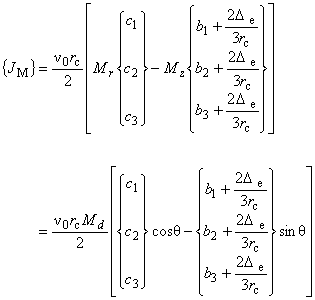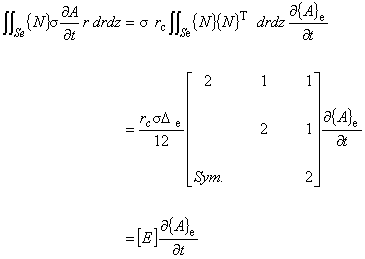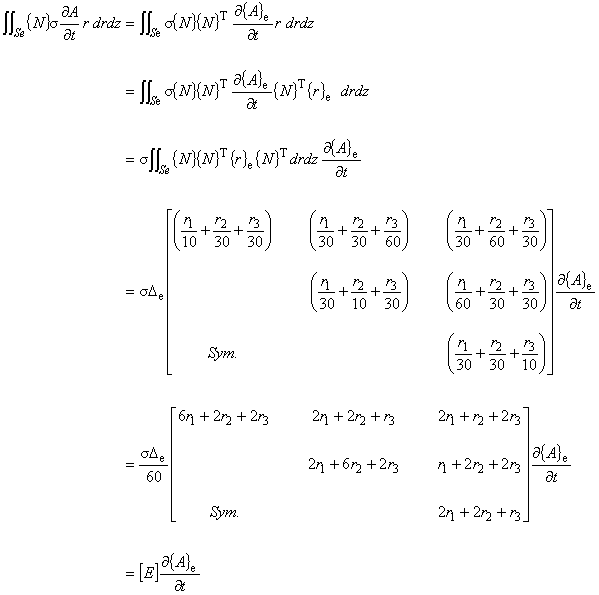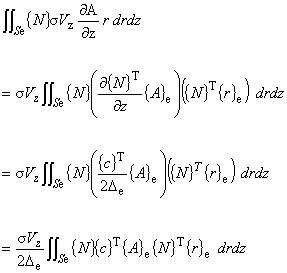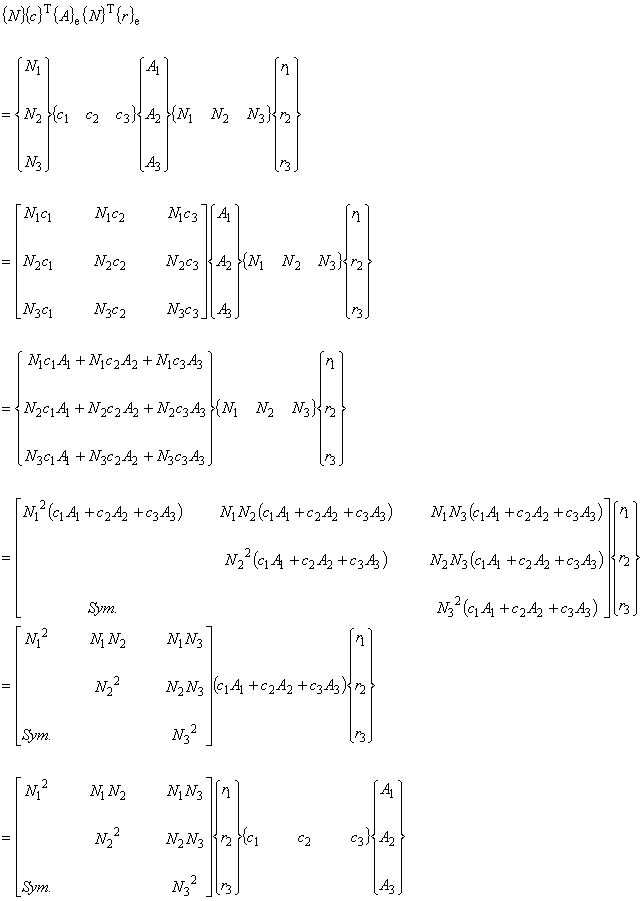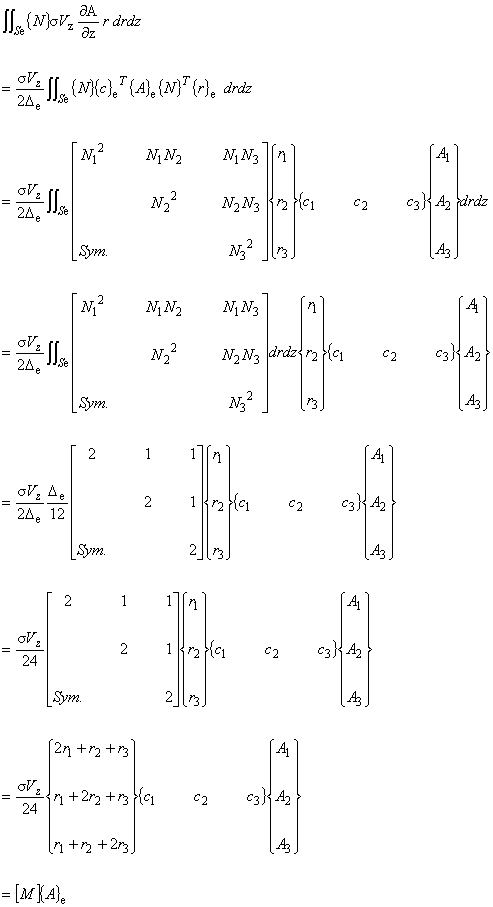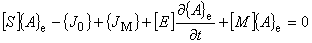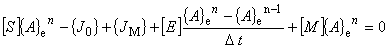|
軸対称磁場解析 6 / 三角形環状1次要素を用いた離散化
|
| 支配方程式にガラーキン法を適用した式 |
|
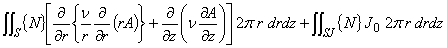
|
(1.18)
|
| および弱形式化した式 |
|
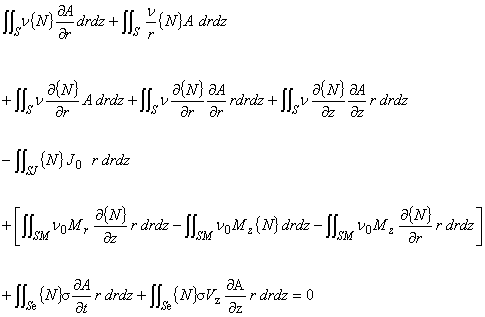 |
(5.2)
|
| に対して,前のページで準備した積分計算を順次適用し,三角形環状 1 次要素を使用した場合の離散化式を求めます。 |
|
一度に考えるのは大変ですので,ここでも項ごとに考えてみます。
まず式(5.2)の左辺第 1 項についてです.式(5.5)を使って計算します。
|
|
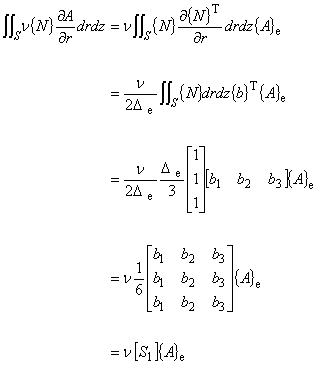 |
(6.1)
|
次は,式(5.2)の左辺第 2 項について考えます。
式(5.11)を使って計算します。
|
|
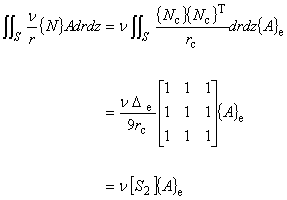 |
(6.2)
|
次は式(5.2)の左辺第 3 項について考えます。
式(5.6)を使って計算します。
|
|
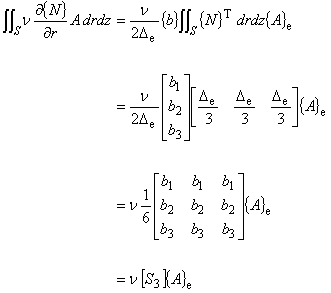 |
(6.3)
|
次は,式(5.2)の左辺第 4 項ついて考えます。
式(5.6)を使って計算します。
|
|
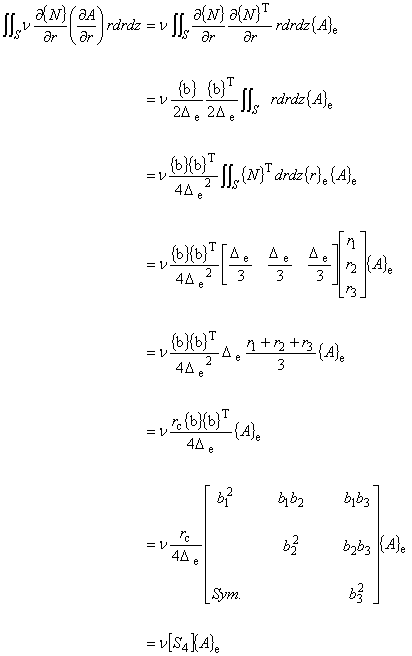 |
(6.4)
|
次に式(5.2)の左辺第 5 項について考えます。
式(5.6)を使って計算します.
|
|
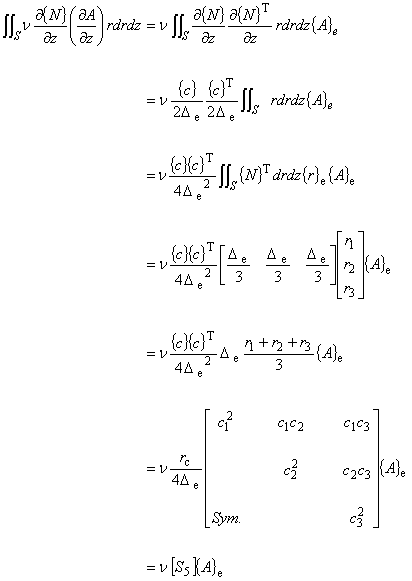 |
(6.5)
|
| 式(6.1)−(6.5)は静磁場項を表しており,まとめると次のようになります。 |
|
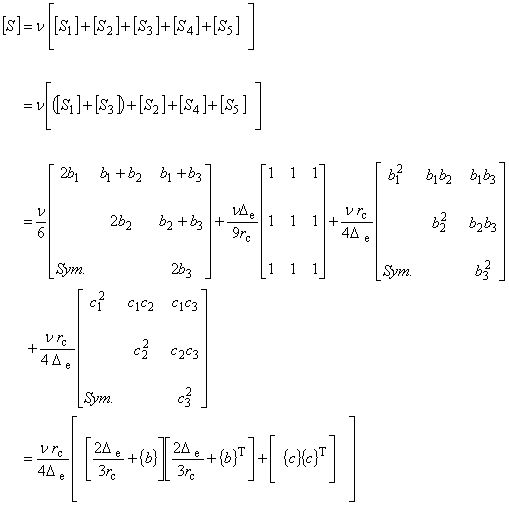 |
(6.6)
|
次は,式(5.2)の左辺第 6 項の駆動電流密度項について考えます。
式(5.7)を使って計算します。
|
|
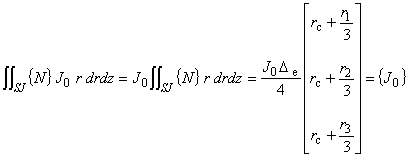 |
(6.7)
|
次は,式(5.2)の左辺第 7 項の等価磁化電流密度項について考えます。
r − z 平面における直交異方性を考慮した式は次のようになります。
これは式 (5.5) と (5.6) を使って計算します。
|
|
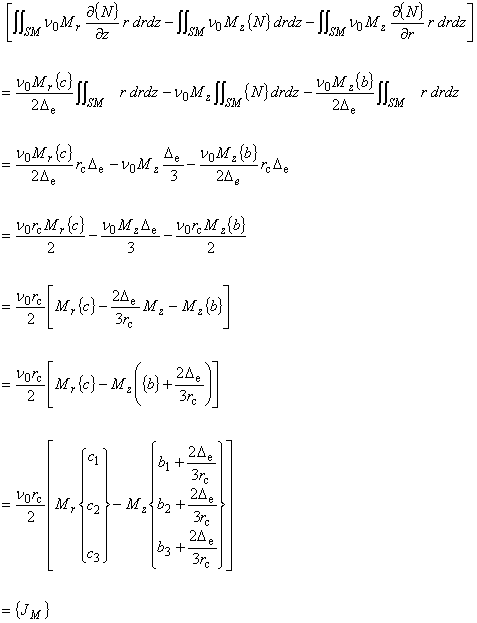 |
(6.8)
|
| ここで,2 次元場のときと同じように任意の磁化方向を考慮する場合は, 磁化の大きさを Md
とし,磁化方向と r 軸とのなす角を θ とすると, 磁化について次の関係があることがわかります。 |
|
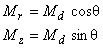 |
(6.9)
|
これを式(6.8)に代入すると,磁化方向を与える場合の等価磁化電流密度項の表現が得られます。
この表現は主に永久磁石領域に適用されます。
|
|
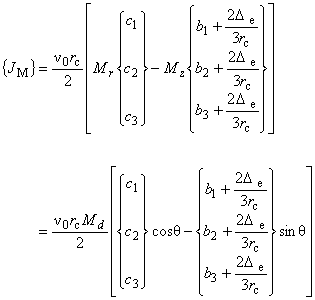 |
(6.10)
|
次に,式(5.2)の左辺第 8 項の渦電流項について考えます。
r を要素の重心の r 座標 rc で近似する方法と,積分に含めて評価する方法があります。
はじめに重心で近似する方法を説明します。式 (5.5) と (5.6) を使って計算します。
|
|
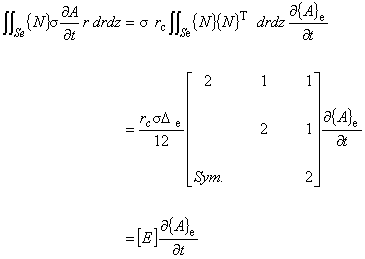 |
(6.11)
|
r を積分対象に含めて評価する方法だと以下のうようになります。
式の導出はこちら。
|
|
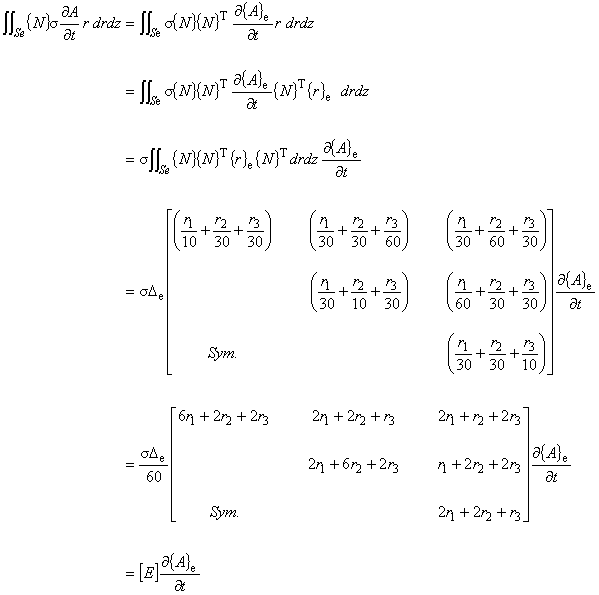 |
(6.12)
|
次に,式(5.2)の左辺第 9 項の運動に起因する渦電流項について考えます。
まず行けるところまで行ってみます。
|
|
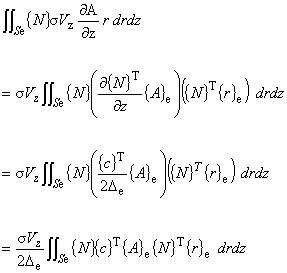 |
(6.13)
|
| 被積分関数について考えてみます。 |
|
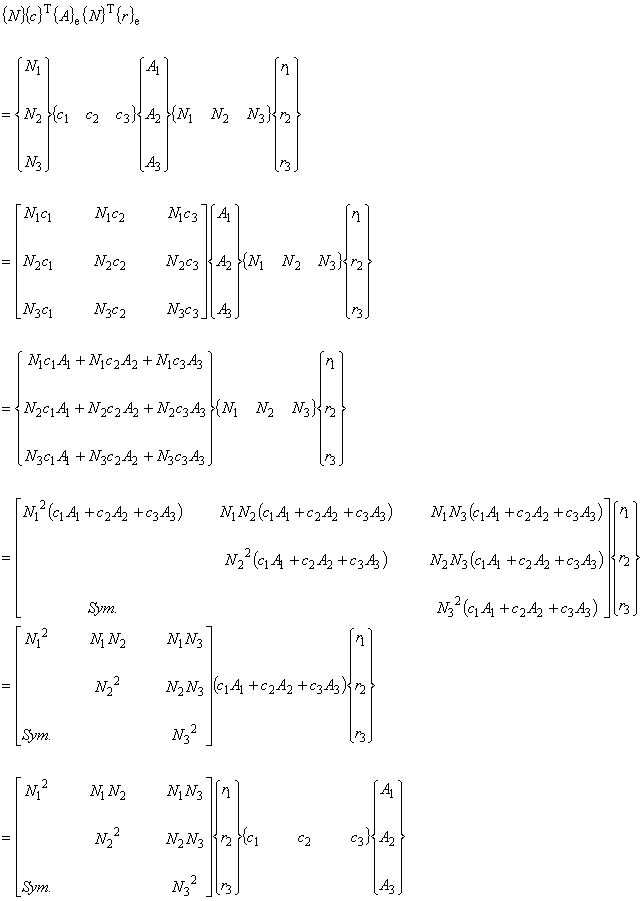 |
(6.14)
|
式 (6.14) を式 (6.13) に代入します。
積分には,式 (5.7) を使います。
|
|
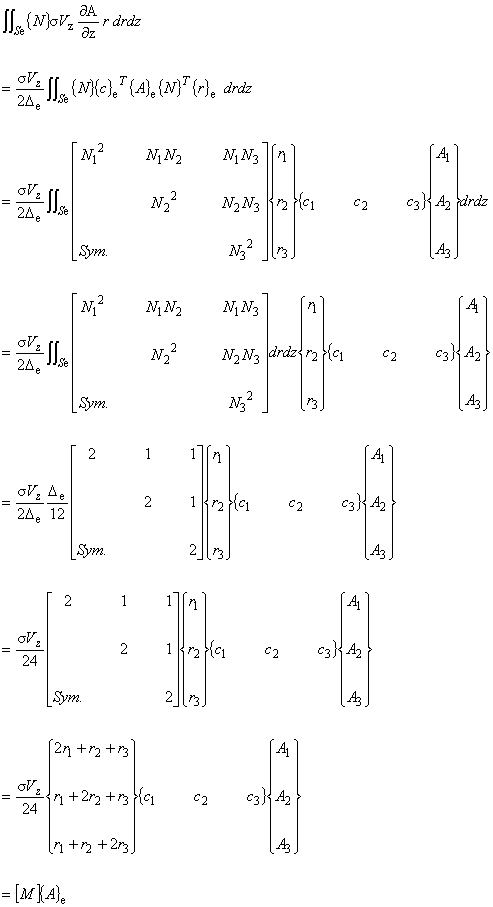 |
(6.15)
|
[M] は非対称行列になることに注意してください。したがってこの項を導入する際は連立一次方程式のソルバーに 非対称行列を解くことができるプログラムを使用する必要があります。
以上で,軸対称場の支配方程式にガラーキン法と三角形環状 1 次要素を用いた離散化式の各項が求まりました。
有限要素式は以下のようになります。
|
|
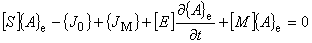 |
(6.16)
|
| ここで,時間項を一階の後退差分で近似すると次のように表されます。 |
|
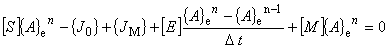 |
(6.17)
|
| 肩の添え字 n は現在のタイムステップでの値を意味します。 |
|
|
|