軸対称磁場解析 5 / ガラーキン法による離散化
支配方程式にガラーキン法を適用した式

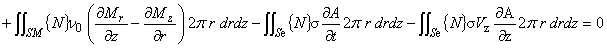
（1.18）
に，次式に示す左辺第 1 項の静磁界項を弱形式化した式
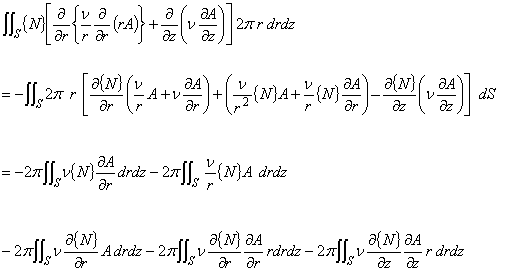
（2.18）
および左辺第 3 項の等価磁化電流密度項を弱形式化した式
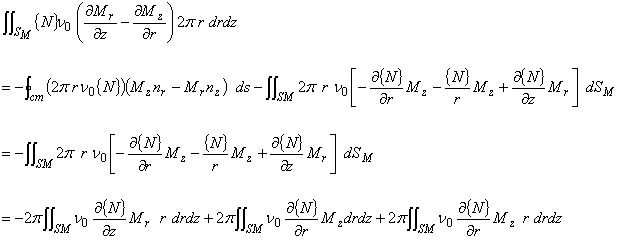
（3.13）
を用いて書き直すと次のように変形されます。
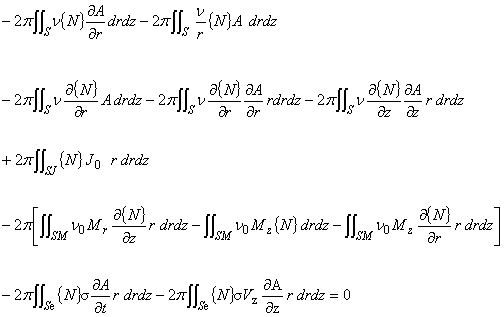
（5.1）
式(5.1)の両辺を−2πで割ります。
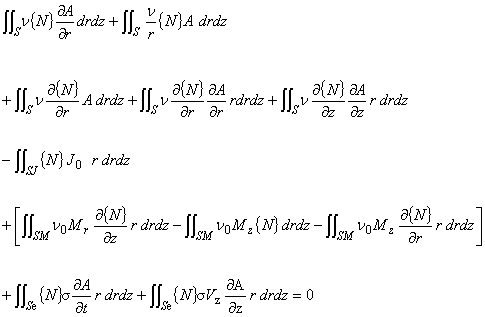
（5.2）

　離散化は三角形環状1次要素を使用します。
ところで，軸対称場の離散化では，分母に r 座標が入っている項があります。
したがって，r ＝ 0 のときには不定となるため積分が実行できません。
そこで，一般的に「場に対して要素分割が十分細かいならば r 座標値を，要素の重心の r 座標値 rc で代表しても精度的に十分である」という近似が行なわれます。
ここで，要素の重心の r 座標 rc は次式により計算されます。

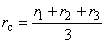
（5.3）
　以上より，軸対称場は 2 次元場と若干離散化の計算が異なるので， 各項の離散化に必要な 4 種類の計算について，ここで前もって準備しておくことにします。
　三角形環状 1 次要素内において，任意点での r 座標値は，要素の補間関数 {N} と要素の節点での r 座標 {r}eより次のように近似します。
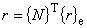
（5.4）
まず，1 番目の計算を示します。
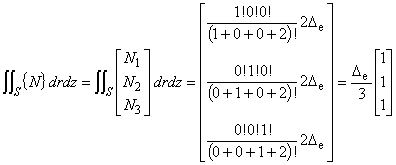
（5.5）
次に 2 番目の計算を示します．
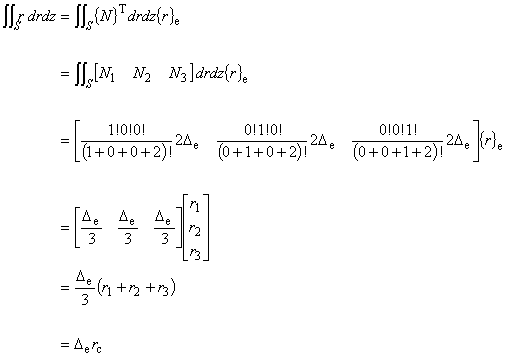
（5.6）
次に3番目の計算を示します．
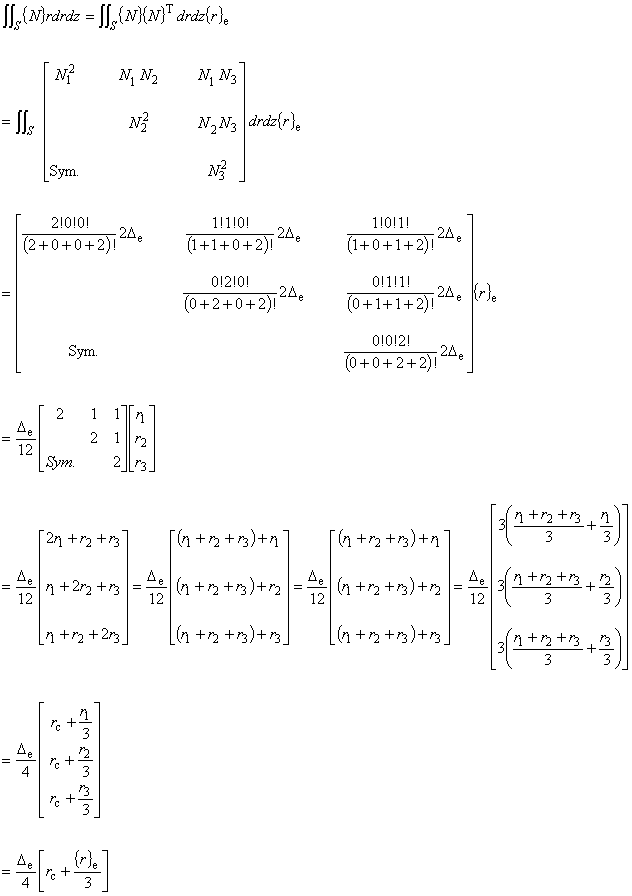
（5.7）
次に4番目の計算を示します。
この計算では，分母の r を要素重心の r 座標 rc で近似します。
したがって，補間関数も要素重心の値で近似します。
要素の補間関数 {N} の各成分は次の式で表されます。
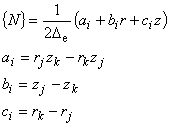
（5.8）
ここで，添字は循環するものとします。
要素重心における N1c は，重心座標 ( rc , zc ) を代入すれば次のように求めることができます。
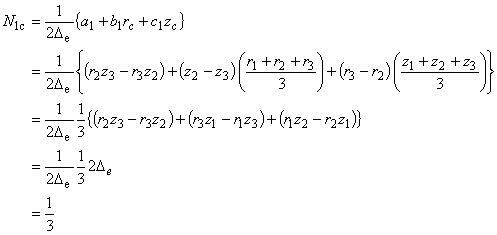
（5.9）
N2c ，N3c についても同様に 1/3 となります．したがって，
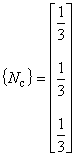
（5.10）

分母を rc で近似した項の内挿関数は式（5.10）のようになります。
これより，4番目の計算は次のようになります．

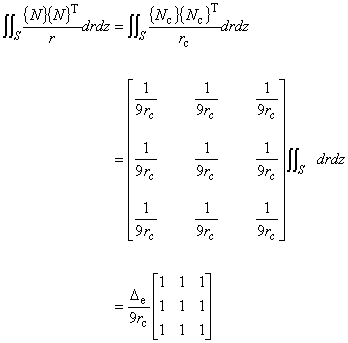
（5.11）
以上，三角形環状一次要素による離散化計算に必要となる計算式 (5.5),(5.6),(5.7),(5.11) の 4 式が求まりました．