軸対称磁場解析 2 / 支配方程式の弱形式化
軸対称問題の支配方程式にガラーキン法を適用すると，支配方程式は次の式で表されることがわかりました。

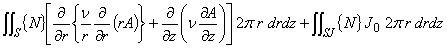
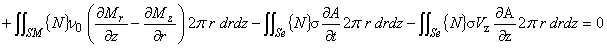
（1.18）
ここでは，式(1.18)の左辺第 1 項の取り扱いを考えます。
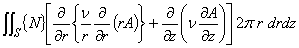
(2.1)
式（2.1）は，2 階微分の項があるので弱形式化して，1 階微分形に次数を下げるように変形します。
これには，2次元場の時と同様に部分積分します。
そのために次のスカラー関数 U と V の関係を示す公式を考えてみます。

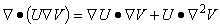
(2.2)
この公式を次のように変形します。
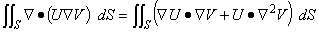
(2.3)
ここで式(2.3)の左辺を眺めながら，次のグリーンの定理を考えます。
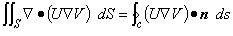
(2.4)
式(2.4)を式(2.3)の左辺に適用して次の式を得ます。
公式との対応をわかりやすくするために積分の文字を dr dz = dS と置き換えてありますが 式の意味は同じですのであまり気にしないで下さい。
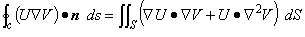
(2.5)
この式を整理した次の形が部分積分の公式になります。
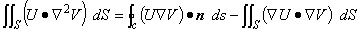
(2.6)
この部分積分の公式で
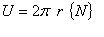
(2.7)
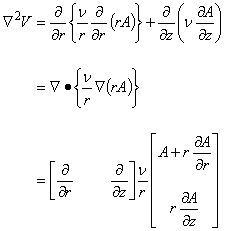
(2.8)
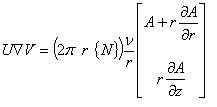
(2.9)
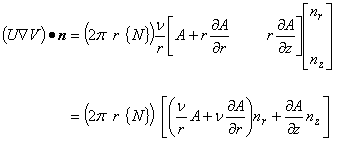
(2.10)
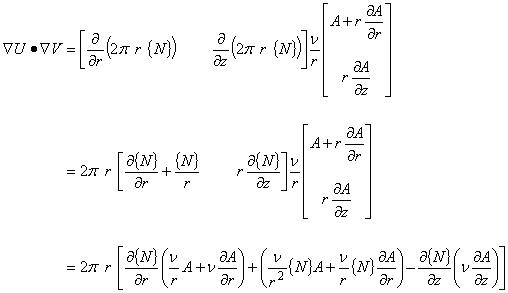
(2.11)
と考えれば，式（2.6）は次のように変形されます。
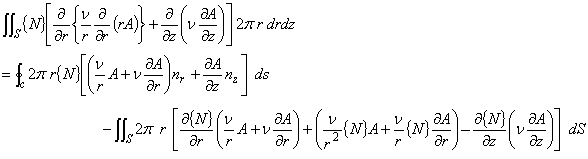
(2.12)
式(2.12)の右辺第 1 項は境界積分項です。
有限要素法による磁場解析では，この項は通常 0 として扱います。
磁界 H [A/m] は次のようにあらわすことが可能です。
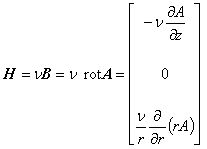
（2.13）
有限要素領域の境界Γ上の法線ベクトルを n とし， その r , z 方向成分を nr,nz とします。
ここで，H と n の外積を考えると，
（2.14）
であることがわかります．
磁界 H が境界に対して垂直になるような条件は，
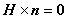
（2.15）
です。
したがって，
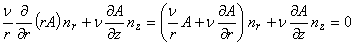
（2.16）
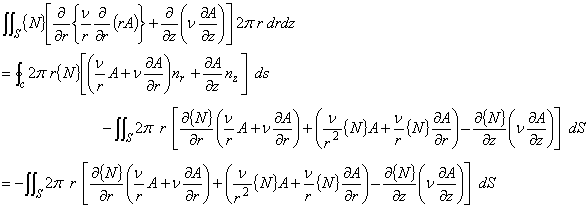
であるので，式(2.12)の右辺第 1 項の境界積分は 0 となり次式が得られます。
（2.17）

　磁界 H が境界に対して垂直となるような条件とは，磁束が境界外部と連続であることを 補償している自然境界条件を意味しています。
磁束は無限遠に拡散しており，これはまた連続です。すなわち div A = 0 です。
有限要素法では解析領域を適当な領域で打ち切らざるを得ません。
このため，有限要素領域とその外側に広がる遠方領域との間で物理量の連続性が補償されねば， 数値解析は物理現象を再現したことにはなりません。
したがって，外部とのつながりを要求される有限要素境界では自然境界条件が設定されるようにします。
一般に有限要素法による磁場解析では，境界条件が陽に与えられない有限要素境界は， 全てこの自然境界条件が自動的に満たされることとなります．

ここで，式(2.17)の右辺を展開すると，

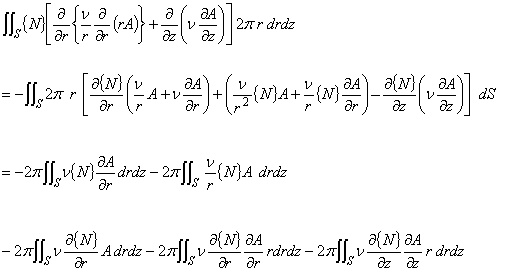
（2.18）
以上より，式(1.18)の静磁場項である左辺第 1 項は，弱形式化され式(2.18)のように 表されることがわかりました。