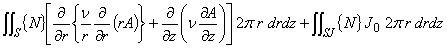
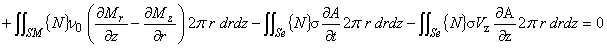
(1.18)
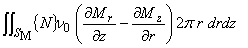
(3.1)
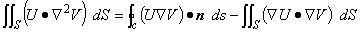
(3.2)
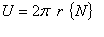
(3.3)
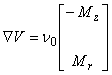
(3.4)
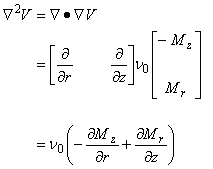
(3.5)
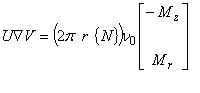
(3.6)
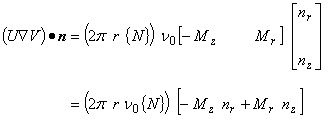
(3.7)
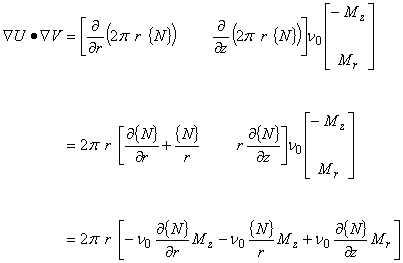
(3.8)
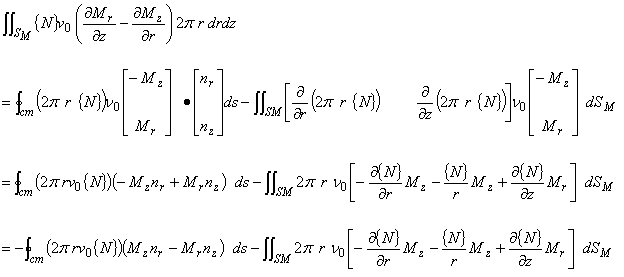
(3.9)
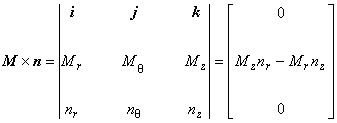
(3.10)
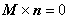
(3.11)
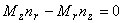
(3.12)
これは,等価磁化電流密度項にガラーキン法を適用し,弱形式化した式を表します。
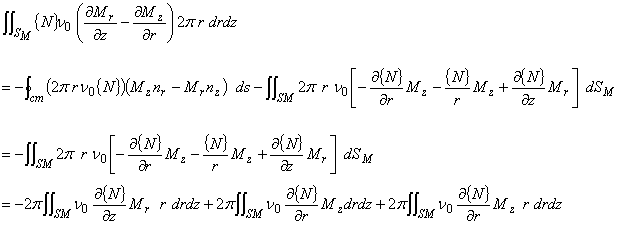
(3.13)
| 軸対称磁場解析 3 / 等価磁化電流密度項の弱形式化 | |
| 軸対称問題の支配方程式にガラーキン法を適用すると,支配方程式は次の式で表されます。 | |
|
|
(1.18)
|
| ここでは,式(1.18)の左辺第 3 項の取り扱いを考えます。 | |
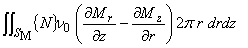 |
(3.1) |
| 左辺第 1 項のときと同様にして,次のスカラー関数 U と V の面積積分の公式を考えます。 | |
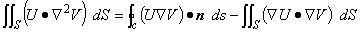 |
(3.2) |
| この部分積分の公式で次のような置き換えを考えます。 | |
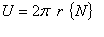 |
(3.3) |
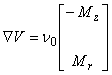 |
(3.4) |
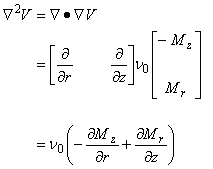 |
(3.5) |
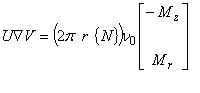 |
(3.6) |
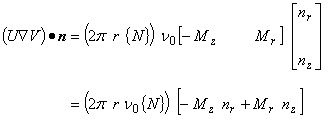 |
(3.7) |
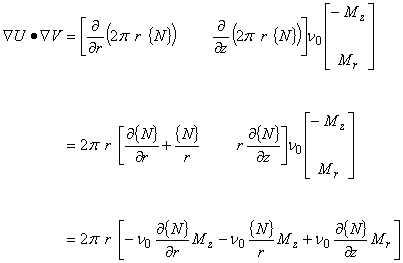 |
(3.8) |
| 式(3.1)を式(3.2)−(3.8)を用いて変形します。 | |
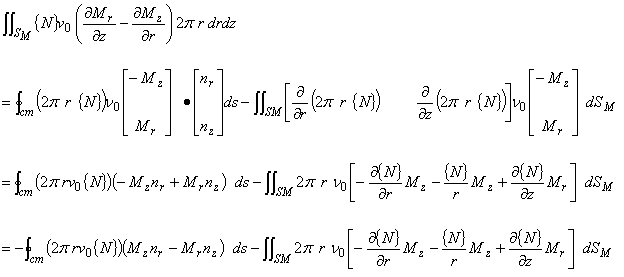 |
(3.9) |
| ここで,磁性体の磁化ベクトル M と境界上の法線ベクトル n の外積は, 軸対称場において次のようになります。 | |
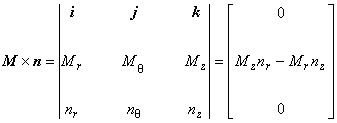 |
(3.10)
|
| 磁性体の磁化が境界に垂直となるような条件 | |
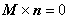 |
(3.11)
|
| すなわち, | |
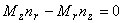 |
(3.12)
|
| を,式(3.9)の右辺の境界積分項に適用すれば,次式が得られます。 これは,等価磁化電流密度項にガラーキン法を適用し,弱形式化した式を表します。 |
|
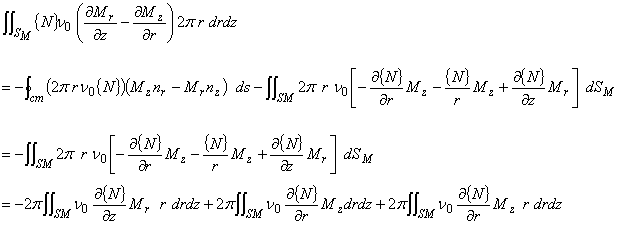 |
(3.13)
|