軸対称磁場解析 1 / 支配方程式と定式化
　軸対称場とは，一般的に円筒座標系 r−θ−z において，z 軸を中心軸に 物理量の θ 方向分布は一様であるという仮定をする場と考えればよいでしょう．したがって，θ 方向には物理量の変化はなく一定であるとします．そのため物理量の変化は r − z 断面についてのみ考えればよく，2 次元場解析とほとんど同じ扱いで軸対称な 3 次元場の解析ができることになります．
次に 2 次元場の時と同じ手順で有限要素式を求めてみましょう．
軸対称場の磁場の支配方程式は，磁気ベクトルポテンシャルを A [ Wb / m ] ，磁気抵抗率を ν [ m / H ] ， 駆動電流密度ベクトルを J0 [ A / m2 ]， 等価磁化電流密度ベクトルを JM [ A / m2 ]， 渦電流密度ベクトルを Je [ A / m2 ] とすると次式で表されます。
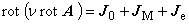
(1.1)
ここで JM と Je はそれぞれ次のようになっています。

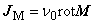
(1.2)

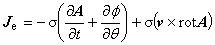
(1.3)
式（2）の M [T] は永久磁石などの磁化を表します。
式（3）について，軸対称場では，スカラーポテンシャルの項は 0 としてよいので，次のようになります。
右辺第 1 項は交番磁場の影響を，第 2 項は導体の運動による渦電流の影響を表します。

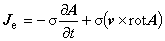
(1.4)
ここで，σ [ S / m ] は導電率，v [ m / s ] は導体の運動速度を表します。

ところで，円柱座標系におけるスカラーポテンシャル φ の勾配（gradient）， およびベクトルポテンシャル A の発散（divergence）， 回転（rotation）はそれぞれ以下のように定義されます。

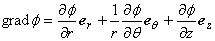
(1.5)

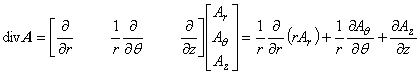
(1.6)

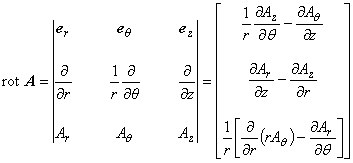
(1.7)
磁気ベクトルポテンシャル A [ Wb / m ] により記述された支配方程式（1）に， 式（2）および（3）式を代入すると次のようになります。

(1.8)
はじめに，式（1.8）の左辺について計算します。
磁場 B [T] は，ベクトルポテンシャル A の回転であるから 円柱座標系の公式（1.7）を参照すれば次の関係があります。

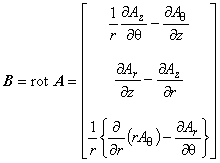
(1.9)
ここで，軸対称場ではベクトルポテンシャル A は θ 方向成分のみを有するとことになります。
そして，物理量は θ 方向には一様であるとしました。
これは軸対称場では，次のような仮定を導入することを意味しています。
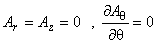
（1.10）
(1.10)を式(1.9)に代入することで軸対称場における磁場 B は次のように表されます。
（1.11）
以上より軸対称場では，磁場 B は r および z 方向成分を有し，それぞれ次のようになります。
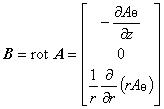
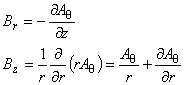
（1.12）
ここで，磁性体の磁気抵抗率 ν [m/H] は等方性を仮定します。
式（10）を考慮して式（8）の左辺を計算すると，次のように表されます。
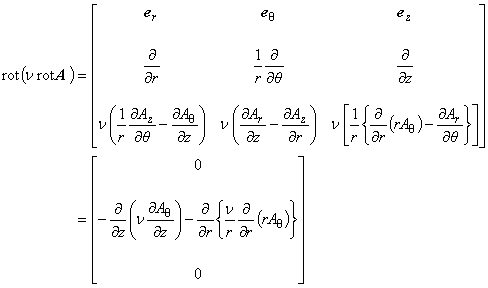
（1.13）
以上より，式（8）の左辺の具体的な成分が求まりました。
磁化ベクトル M についても A と同様に計算でき，軸対称場では次のように表されます。
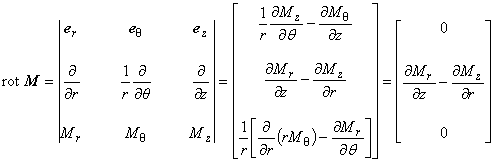
（1.14）
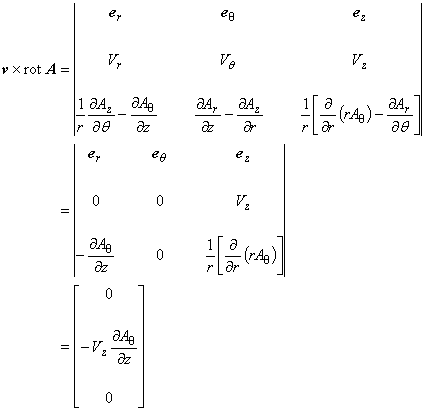
式（8）の右辺第 3 項は，導体の運動による渦電流を表す項でありますが， 運動は z 軸方向のみと仮定すると次のように成分が計算できます。
（1.15）
これより先，軸対称場の解説において，以降は Aθ は特に断らない限り A と表記します。
式（8）に，式（11），（13），（14）を代入して整理すると，支配方程式は次のように表されます。
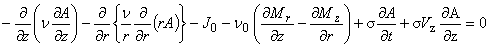
（1.16）
両辺に−1をかけると次のようになります。
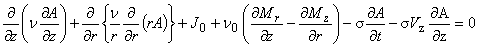
（1.17）
ここで，要素の補間関数を｛N｝とします。
｛N｝を重み関数に採用するガラーキン法の式は次のように表されます。
軸対称場であるので 2πr 倍されていることに注意してください。
また {N} は重み関数であり単位は無次元です。

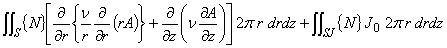
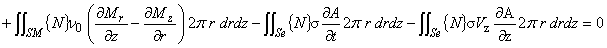
（1.18）
なお積分領域は次のように考えてください．
S ：有限要素領域全体
SJ ：コイル要素領域
SM ：永久磁石などの磁化のヒステリシスを考慮する領域
Se ：渦電流が流れる導体領域