図 1 に直交座標系での六面体一次要素を,図 2 に正規化された局所座標系における六面体一次要素を示します。
一般に,要素の節点数が増えると直交座標系で数値計算を進めることは計算の手数が増えるため得策ではありません。
そこで,要素ごとの積分計算は正規化された局所座標系において行ない,その結果を全体座標系に写像変換するという方針が採られます。
ここでは熱伝導マトリックス [K] を取り扱いその過程を追ってみます。
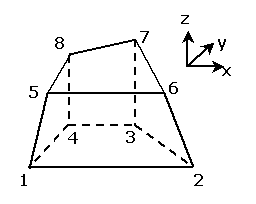
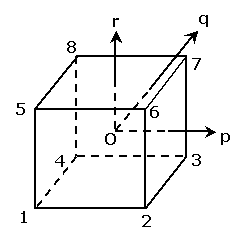
図 1 全体座標系での要素 図 2 局所座標系での要素
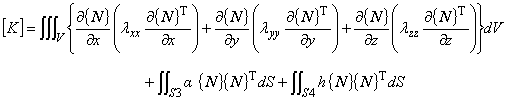
熱伝導マトリックス [ K ] において,次のことを理解しておきます。
1:マトリックスの計算には積分が要求されいること
2:被積分関数は直交座標系で定義されていること
3:計算機で積分計算を行なう場合,数値積分というテクニックが使用されるということ
4:数値積分は,被積分関数を局所座標系で定義しておくことで容易に行なうことができるということ
それゆえ,実際の積分計算は,被積分関数を直交座標系から局所座標系に変換してから数値積分を行ないます。
三次元解析では,要素の積分計算を全体座標系で行なうのではなく,局所座標系で行なうことは理解できたでしょうか。
もう一度流れを説明すると,局所座標系で積分計算を行ない,それを全体座標系に写像変換を行なうというプロセスが採用されます。
したがって,ここからは局所座標系( p‐q‐r )における定式化の手順を説明します。
温度 T はスカラー補間関数 { N } を用いてそれぞれ次のように表されます。
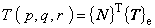
ここで {T}e は要素の節点温度です。
また,各節点に定義される補間関数 {N} の成分は,局所座標の関数として次のように与えられます。
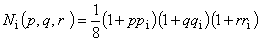
ただし,
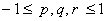
です。
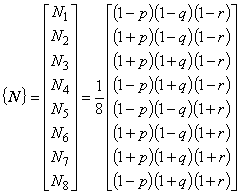
補間関数 {N} の各成分の局所座標系における偏微分が必要になります。
そこでこれらを求めると以下のようになります。
|
p による偏微分
|
qによる偏微分
|
rによる偏微分
|
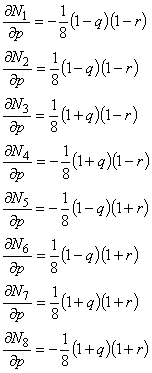 |
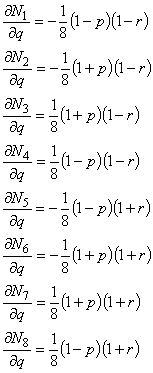 |
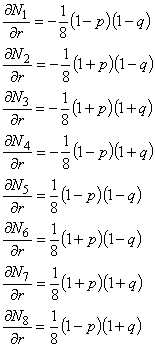 |
六面体1次アイソパラメトリック要素では,全体座標と局所座標は補間関数 {N} と要素の節点座標
( xyz 座標系) {x}e {y}e {z}e を用いて次のように補間されます。
右辺の節点座標ベクトル {x}e,{y}e,{z}e は,節点座標ですから要素分割時に定義されるので既知のベクトルといえます。
一方,左辺の座標 x,y,zは,{N} という p,q,r を変数に持つ補間関数によって表されていることから,p,q,rの関数であるといえます。
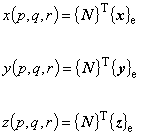
ただし,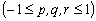
したがって,直交座標系での偏微分と局所座標系での偏微分は次の式で関係付けられます。
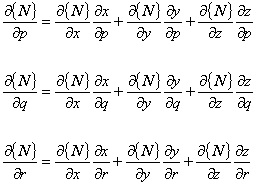
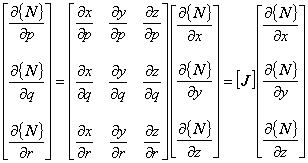
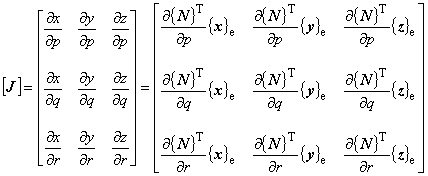
離散化過程で要求されているのは,式(8)の右辺にある全体座標系での補間関数の偏微分です。
式(8)より,補間関数の偏微分に関して全体座標系と局所座標系での変換は次の式で表されます。
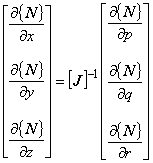
式(10)より,全体座標系での補間関数の偏微分を求めるためにはヤコビ行列の逆行列を求めておく必要があります。
ヤコビ行列の逆行列は次のようになります。
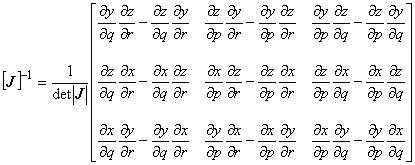
ここで
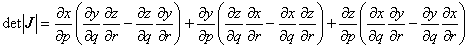
です。
式(11)を式(10)に代入すると,

したがって,全体座標系における偏微分は次の3式で評価されることになります。
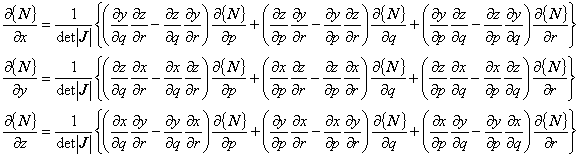
これは,局所座標系で求められた物理量を全体座標系での値に変換するために必要になります。
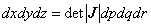
***
六面体要素では,境界面は六面から構成されています。
局所座標において p , q , r のどれかが一定となるように定義することができます。
(p=±1のとき)
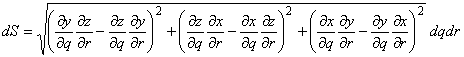
(q=±1のとき)
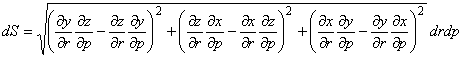
(r=±1のとき)
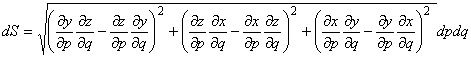
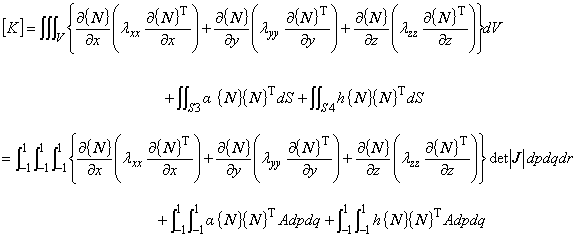
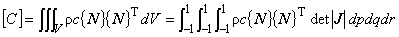
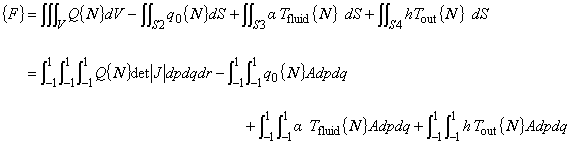
以上より各マトリックス及びベクトルの被積分関数の変換式が示されたので,数値積分を行なうことができるようになります。
ここでの数値積分は,
1: 被積分関数をf(p,q,r)
2: 局所座標系における分点座標を( pi,qj,rk)
3: 分点における重みを( Wi,Wj,Wk)
4: 分点の数を n
とすると,体積積分及び面積積分は次のようになります。
体積積分
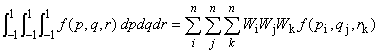
面積積分
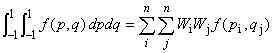
分点数は 2〜3ほどとれば精度的には十分です。
非定常解析における時間微分項について,1 階の後退差分で近似した場合には有限要素式は次のように表されます。
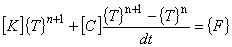
時刻 n における節点温度 {T}n まで求まっているものとすれば,この項は既知量となります。
したがって,未知温度と既知量を分離すると次のような式が得られます。
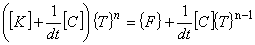
ただし, 時間方向の解像度である dt を大きくすると得られる解の精度は当然低下します。
有限要素法では,空間部分の離散化はメッシュにより行い,メッシュサイズが小さいほうが精度が良くなることは一般的に知られています。
同様にして,時間方向の離散化も dt を小さくするほうが精度が良いことが理解できると思います。



