固体の3次元熱伝導解析
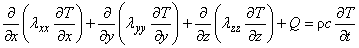
|
T
|
温度 (Temperature) | [ ℃ ] |
|
λ
|
熱伝導率(Thermal conductivity) | [ W / m ℃ ] |
|
Q
|
内部発熱率 | [ W / m3 ] |
|
ρ
|
密度 (density) | [ kg / m3 ] |
|
c
|
比熱 (specific heat) | [ J / kg ℃ ] |
|
t
|
時刻 (time) | [ s ] |
(1.1)
したがって支配方程式は非線形方程式となります。
しかしながらこれらの温度依存性は数十度の範囲では小さいことが多く,ここでは簡単のため無視します。
熱伝導問題の境界条件は,熱流速を q [ W / m2 ],境界上での外向きの法線ベクトルを n とするとフーリエの法則より次の式で与えられます。
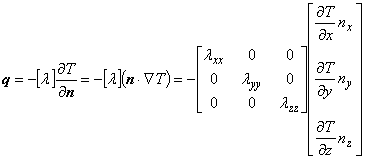
(1.2)
ここで,重み関数は{N}とします。
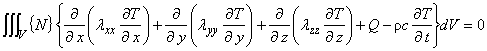
(1.3)
上式について,次のように 3 つの項に分けて考えていきます。
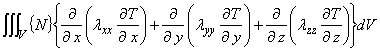
(1.4)
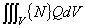
(1.5)
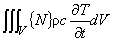
(1.6)
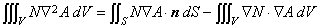
(1.7)
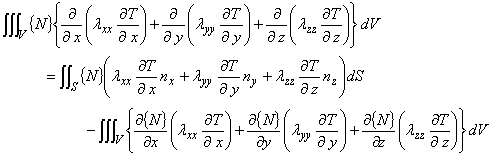
(1.8)
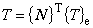
(1.9)
ここで,節点温度は空間の関数ではないので,積分の外へ出されることに注意して下さい。
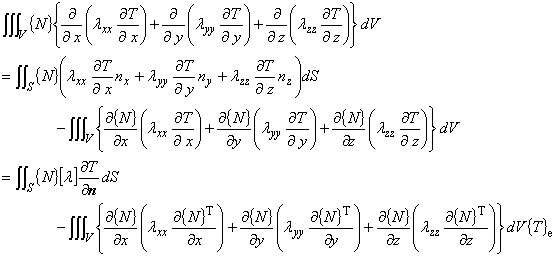
(1.10)
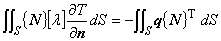
(1.11)
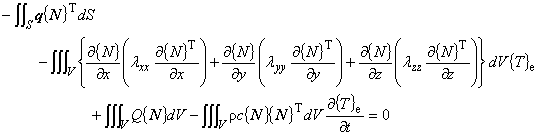
(1.12)
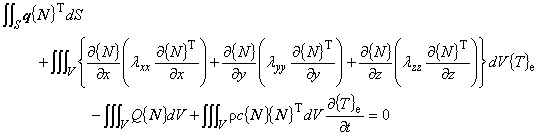
(1.13)
となります。
次に離散化式に境界条件の影響を評価する項を導入します。
一般に熱伝導問題の境界条件に関しては,温度固定条件,熱流速条件,熱伝達条件,熱輻射の4つの条件を考慮します。
境界 s1 上において
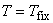 on s1
on s1
(1.14)
ここで Tfix は固定温度です。
熱流速境界条件とは,境界 s2 上で熱流速 q0 [ W / m ℃ ] が流出入するという境界条件であり,次のように与えられます。
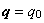 on s2
on s2
(1.15)
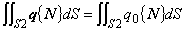
(1.16)
「境界 s3 上で固体表面と周囲を流れる流体との間で熱伝達が行われるという条件」で,
熱伝達率を α [ W / m2 ℃ ] ,周囲流体温度を Tfluid [℃] とすると次のように与えられます。
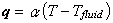 on s3
on s3 (1.17)
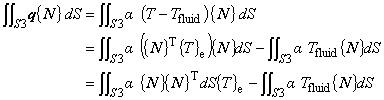
(1.18)
「固体の境界 s4 上で周囲環境に対して熱輻射が行われる」という境界条件で,
熱輻射率を h [ W / m2 K] ,周囲環境温度を Tout [K] として次のように与えられます。
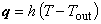 on
s4
on
s4 (1.19)
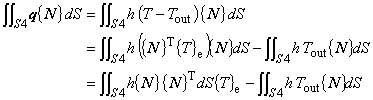
(1.20)
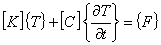
(1.21)
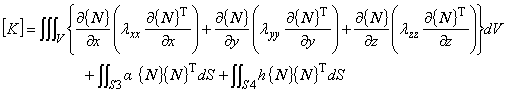
(1.22)
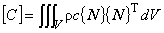
(1.23)
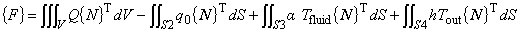
(1.24)
です。
[K] は熱伝導マトリックス
[C] は熱容量マトリックス
{F} は熱流速ベクトルです。
以上で有限要素式が得られました。
有限要素式の具体的な成分は要素によって内挿関数 {N} が異なるので,使用する要素に応じて定式化を行なう必要があります。
ここでは,六面体一次要素の場合について定式化を進めていきます。



