物性値
領域1の熱伝導率 λ1 :0.385 [ W / mm℃ ] (銅を想定)
領域2の熱伝導率 λ2 :0.073 [ W / mm℃ ] (鉄を想定)
r1 : 50 [mm] r2 : 100 [mm] r3 : 150 [mm] h:50 [mm]
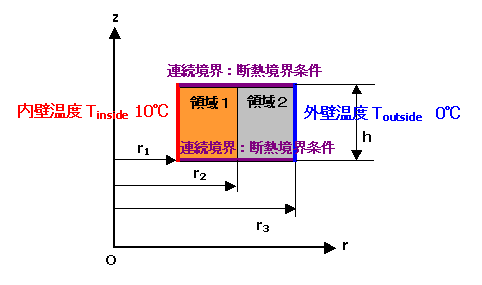
図1 解析モデル
温度分布グラフ
■領域1における半径 r の点での温度分布
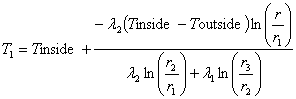
■領域2における半径 r の点での温度分布
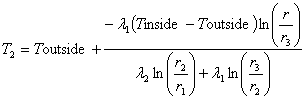
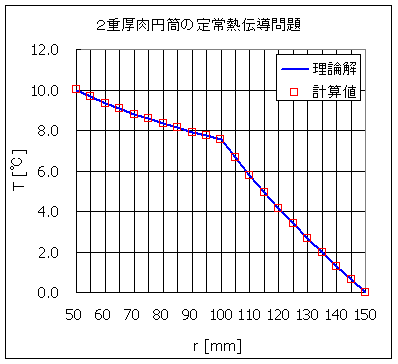
図 3 半径 r における温度分布
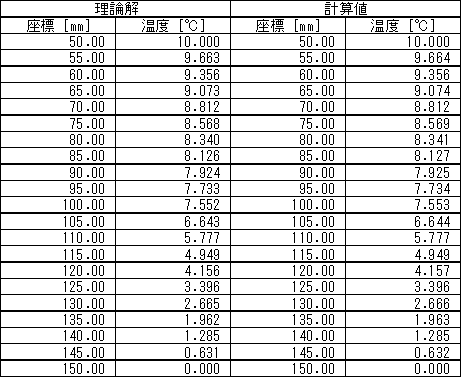
表 1 温度分布の理論解と計算値
| 例題5 温度拘束された2重厚肉円筒の軸対称定常熱伝導解析 | |
| 出典:田中正隆,松本敏郎,中村正行:「計算力学とCAEシリーズ 境界要素法」,培風館,p285-286 | |
| 軸対称/定常/線形/問題 節点数:336 要素数:600(三角形環状1次要素) | |
| 境界条件:温度拘束境界条件 内壁: 10 [℃] 固定,外壁: 0 [℃] 固定 上下方向の連続条件:断熱境界条件 | |
|
物性値 |
|
| 寸法 r1 : 50 [mm] r2 : 100 [mm] r3 : 150 [mm] h:50 [mm] |
|
| 解析モデル ( 軸対称 モデル ) | |
|
図1 解析モデル |
|
| 計算結果 温度分布 | |
|
温度分布グラフ |
|
| 本問題においては,半径方向 r [mm] の温度分布の理論解を次の式により求めることができます。 | |
|
■領域1における半径 r の点での温度分布
■領域2における半径 r の点での温度分布
|
|
|
図 3 半径 r における温度分布 |
|
| 数値データ | |
| 表1に数値データを示します。 | |
|
表 1 温度分布の理論解と計算値
|
|