例題３　厚肉円筒の定常熱伝導解析（熱流速問題）
出典：鷲津，宮元，山田，山本，川井編：「有限要素法ハンドブックⅡ」，培風館，p.460
2次元／定常／線形／問題 　節点数：336　要素数：600（三角形 1 次要素）
境界条件：温度拘束境界条件
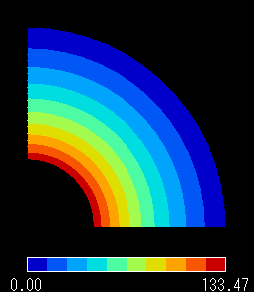
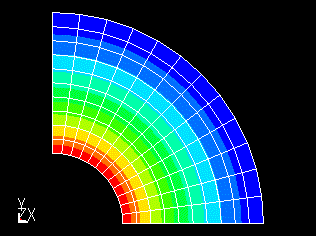
○　外壁：0 [℃] 固定
○　内壁：熱流速境界条件 流入 0.56 [ W / mm2 ] ）( -560.0 [Nmm/sec]*[1/mm2])
○　対称面：断熱境界条件 q = 0 [ W / mm2 ]

物性値
領域１の熱伝導率 λ ：0.230 [ W / mm ℃ ] （アルミを想定）( 230.0 [Nmm/sec]*[1/mm℃])

寸法
r1： 50 [mm]　r2 ： 150 [mm]
解析モデル　（ 1/4 モデル ）

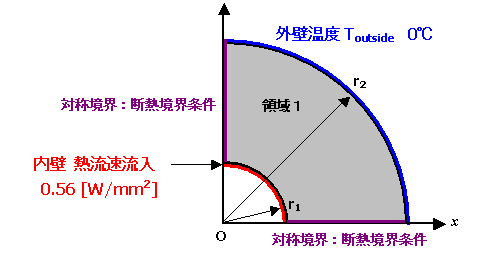
図 1　解析モデル

　
計算結果　温度分布

　

　　

図 2　温度分布　左：自作コード　　右 LS-DYNA による結果

LS-DYNAに関する解析技術のご相談はこちらへ：ランスモア

温度分布グラフ

本問題においては，半径方向 r [mm] の温度分布の理論解を次の式により求めることができます。

■領域１における半径ｒの点での温度分布 T

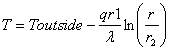
q：熱流速，λ ：熱伝導率，Toutside：外壁温度，r1：内径，r2：外径

　

　

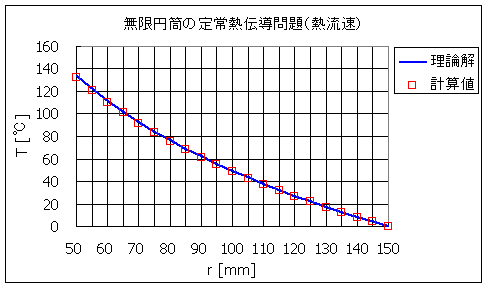
図 3　半径 r における温度分布

数値データ
表 1 に数値データを示します。

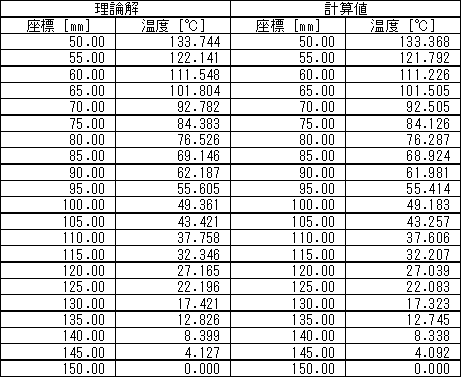
表 1 　温度分布の理論解と計算値