三角形一次要素による離散化

　
要素分割に使用する要素は三角形一次要素とし，物性値や係数が要素内で一定であるとすると，[k]，[c]，{f}はそれぞれ次のように離散化されます。 　
(3.1)
(3.2)
(3.3)
境界積分項は領域積分項に比べて寄与する節点が一つ少ないため，次数が下がっていることに注意して下さい。
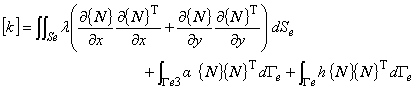
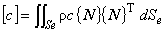
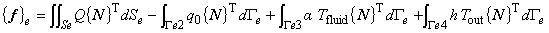
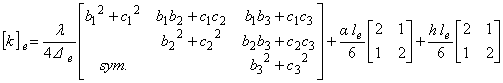
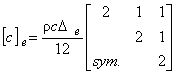
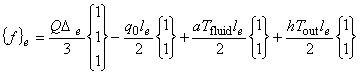
これについて具体的に説明します。 図1に三角形一次要素を示します。		 　

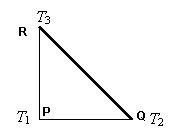
図１　三角形一次要素

 　

三角形一次要素内における任意点の温度 T は，補間関数 N を用いて次の式により近似されています。

 　
(3.4)

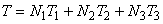
補間関数は線形です．そのため次のことがいえます．

節点Pでの温度 T1 の影響は節点 Q , R において 0 です．
節点Qの温度 T2 の影響は節点 P と R において 0 です．
節点Rの温度 T3 の影響は節点 P 及び Q において 0 です．

以上より，各頂点の温度の影響は対辺上では 0 であることがわかります。
すなわち，境界辺 QR 上では，節点 P の温度 T1 の影響は 0 であるから境界辺 QR 上の任意点における温度 TΓ は，
式(3.4)において T1＝0 として次のように表されます。

　
(3.5)

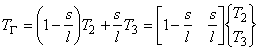
境界辺 QR 上では，節点 Q と節点 R の温度のみが影響していることから上式のようになることがわかります。
したがって，境界積分項においては境界辺を構成する節点の温度の影響のみを考慮すればよいので，領域積分よりも次数が下がることがわかります。

次に，図２を参考に三角形一次要素の個々の境界辺について境界積分項のマトリックスを示します。
なお図で，l1，l2，l3は，境界辺の長さを表します。

　

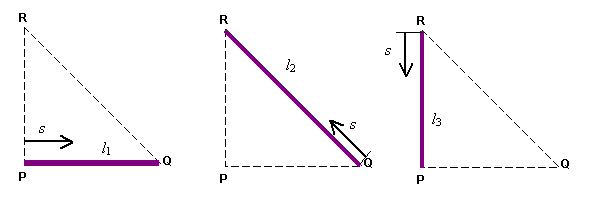
図2　三角形一次要素と境界辺

 　
辺PQが境界辺の場合

(3.6)
(3.7)
境界辺がQRの場合

(3.8)
(3.9)
境界辺がRPの場合
(3.10)
(3.11)

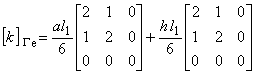
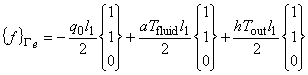
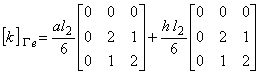
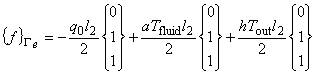
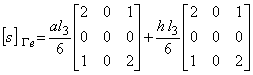
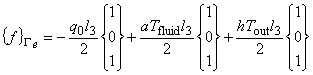
境界積分項の取り扱いについて述べました。
解析プログラムでは，境界に接している要素においてどの辺が境界辺なのかを判断させ，
それに応じて境界条件の影響を要素レベルの有限要素式に導入することになります。

ここまでで，二次元非定常熱伝導解析の有限要素式(3.3.19)を構成するマトリックスとベクトルの成分が明らかになりました。
時間依存項を一階の後退差分で近似すれば，有限要素式は次のように表すことができます。

 　
(3.12)
肩の添え字 n+1 はこれから求める時刻を，n は現在の時刻を表しています。
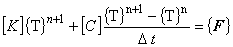
未知数と既知数を分離すると式(3.12)は次のように変形されます。		 　
(3.13)

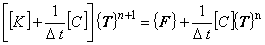
式(3..13)を解くことで，二次元線形非定常熱伝導解析を行なうことが可能となります。
この差分近似は，陰解法であるので数値安定性に関しては無条件安定となり，数値振動を起して解が発散することはありません。
しかしながら，温度の時間変化率が大きい現象で過渡的な状態を追跡したい場合には，
時間増分値 DT を十分小さくしておくことが解の精度を向上させるために必要となります。