有限要素法による固体の熱伝導解析
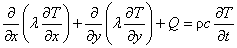
|
T
|
温度 (Temperature) | [ ℃ ] |
|
λ
|
熱伝導率(Thermal conductivity) | [ W / m ℃ ] |
|
Q
|
内部発熱率 | [ W / m3 ] |
|
ρ
|
密度 (density) | [ kg / m3 ] |
|
c
|
比熱 (specific heat) | [ J / kg ℃ ] |
|
t
|
時刻 (time) | [ s ] |
一般に熱伝導率や比熱には温度依存性があり,これらは非線形性を示すため支配方程式は非線形方程式となります。
しかしながら,数十℃程度の範囲では,これらの温度依存性は非常に小さいことも多く,ここでは簡単のため無視します。
さらに熱伝導率にも異方性がありますが,ここでは等方性とした場合について考えます。
以上の場合の熱伝導問題の支配微分方程式は次式のようになります。
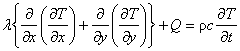
以上の熱伝導問題の支配微分方程式は,定常問題であれば境界条件を与えることで解くことができます。
非定常問題であれば,境界条件のほかに初期条件を与えることで解くことができます。
境界条件としては,
○ 境界上の温度が規定される温度固定条件(ディリクレ条件)
○ 境界上における熱流速 q が規定される条件(ノイマン条件)
に分けることができます.
温度固定条件は,Dirichlet 条件であり温度が規定される節点に与える条件です。
これは,境界 s1 上の温度をある一定温度に固定するというものです。
有限要素法では,物質の初期温度が一様に 0 [℃] で,内部発熱なし,外部と断熱されている系では,固定境界条件を課さないと微分方程式が不定となってエラーが発生します。
この条件は,厳密には温度が規定されているということを判断するのは難しいのですが,境界条件の考え方としてはシンプルですのでよく使用されます。
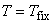 on s1
on s1 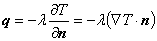
熱流速条件は熱流速,熱伝達,輻射の3つに分類することができます。
まず,熱流速境界条件とは,境界 s2 上で熱流速(熱量) q0 が流出入するという境界条件で次のように与えられます。
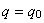 on s2
on s2 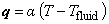 on s3
on s3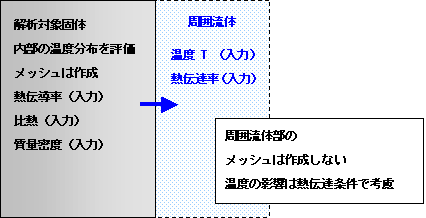
図 熱伝達境界条件のイメージ
熱輻射率を h ,ステファン・ボルツマン定数を σ,形状係数を F,周囲環境温度を Tout として次のように与えられます。
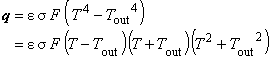
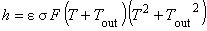
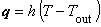 on s4
on s4 以上,二次元線形非定常熱伝導問題の支配方程式と境界条件について述べました。
熱伝導問題の支配方程式と境界条件が明らかになったので,支配方程式をガラーキン法により離散化します.
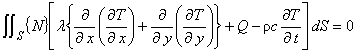
一度に考えると大変なので次のように3つの項に分けて考えます。
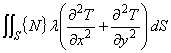 熱拡散項
熱拡散項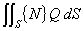 発熱項
発熱項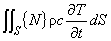 熱容量項
熱容量項ここで式(2.11)は 2 階微分項を含んでいるので部分積分を適用して 1 階微分形式に弱形式化します。
磁界解析のところでも述べたように,次の部分積分の公式を考えます.
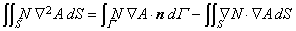
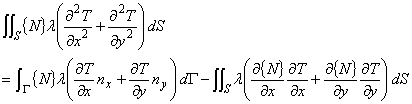
ここで,S は二次元領域,Γはニ次元領域の境界面,nx ,ny は境界面に立てられた外向き法線ベクトルの x, y 方向成分です。
要素内での任意点での温度 T は内挿関数ベクトル {N} を用いて,次のように節点温度ベクト {T}e より近似されます.
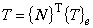
ここで,節点温度は既知量であり空間の関数ではないので,積分の外へ出されることに注意して下さい。
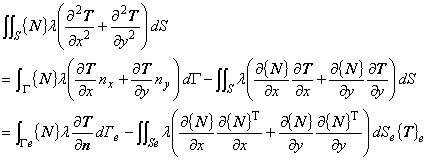
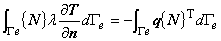
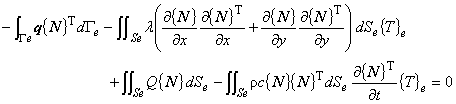
式(2.19)は,個々の境界条件については明確に表現されていません。
そこで,式(2.19)の離散化式に境界条件の影響を評価する項を導入します。
熱伝導問題の境界条件に関しては,先に述べたように温度規定,熱流速規定,熱伝達,熱輻射の4つの条件が一般的です。
ここで,温度規定条件は支配方程式中の温度 T が既知であるという条件のため支配方程式の形はそのままで,
FEMでは連立一次方程式を解く際にマトリックスを処理して考慮します。
熱流速規定境界条件の場合,式(2.19)の左辺第1項に式(2.5)を代入すると左辺第1項の境界積分項は次のように変形されます。
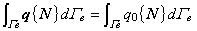
式(2.19)の左辺第 1 項に式(2.6)を代入すると左辺第 1 項の境界積分項は次のように変形されます。
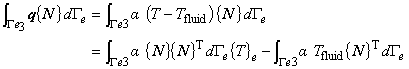
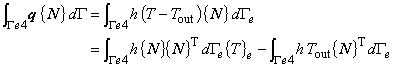
ここで,要素熱拡散マトリックス[k],要素熱容量マトリックス[c],要素熱流速ベクトルを{f}とするとそれぞれ次のように表されます。
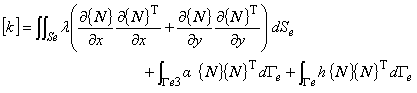
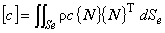
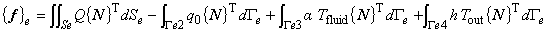
制御工学風にいうと,{ f } が入力信号で,[k]が伝達関数ということになります。もちろん{ T }が出力(応答)信号になります。
以上より,対象領域の各要素について次の要素連立一次方程式を考えたことになります.
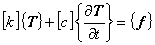
これは多元連立一次方程式であり,ガウスの消去法やICCG法などの連立一次方程式ソルバーにより解きます。
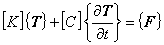
以上により,二次元線形非定常熱伝導問題の有限要素式が得られました。
有限要素式の具体的な成分は使用する要素により補間関数{N}が異なるので,使用する要素に応じて定式化を行なう必要があります。
次からは,三角形一次要素を用いて離散化を進めることにします.



