温度と温度変化率の近似式について

温度と温度変化率の近似式について
時間微分項の離散化に関する説明では，温度と温度の時間変化率を近似する次の式が登場します。ここではこれらの導出方法について説明します。すなわち登場する 2 式は（1）および（2）です。タイムステップ N の時刻を t_n ，N + 1 の時刻を t_{n + 1}とすると N と N + 1 ステップの間における任意の時刻 t はパラメータ θ を用いると

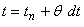
と表すことができ，このステップを仮に N + θ ステップと表現します。このときの温度 T_n+θは，次式で近似されます。
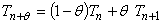
	（1）
また温度の時間変化率は次式で近似されます。
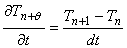
	（2）
ここで，時刻と温度との関係を図1に示します。
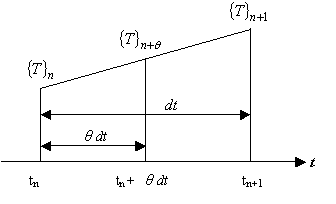
図１　時間と温度の関係
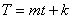
いま，温度を線形近似していますので，傾きを m ，時刻 0 における温度軸に対する切片を k とすれば，時刻 t_n と t_n+1の間で，
	（3）
と近似することができます。図 1 を参考にすれば，時刻 t_n および t_n+1 において温度はそれぞれ次式で表現できます。
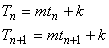
	（4）
となります。（4）式の片々を引くと，

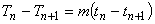
となるので，2 点間の温度勾配 m は
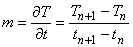
	（5）
であることがわかります。これはまさに式（2）そのものです。温度の時間変化率は t_n と t_n+1 の間で一定であることからも自明です。したがって（2）が導出できました。（dt = t_n+1 - t_n です）（5）を（3）に代入すると次式が得られます。
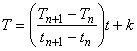
	（6）
となります。切片 k を求めるために，時刻 t_n で温度が T_n であるという関係を代入すれば
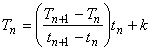
	（7）
k についての形に直すと次のようになります。
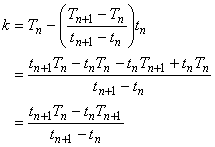
	（8）
（8）を（7）に代入することで，温度と時間の関係は次式で表されることがわかります。
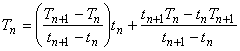
	（9）
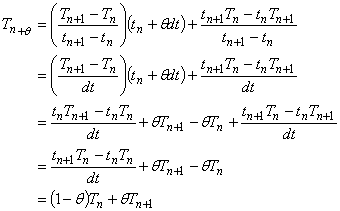
これにより，タイムステップ N + θ における温度 T_n+θ は，次式で表されます。
	（10）
以上で導出が終了しました。