熱伝導解析における時間項の離散化と計算精度について

熱伝導解析における時間項の離散化と計算精度について
有限要素法による非定常熱伝導解析では，空間については有限要素により離散化を行ない，時間方向については差分法で行ないます。空間についてはメッシュサイズを小さくするほど解像度が良くなるため解の精度が向上することは良く知られていますが，同様に時間方向のタイムステップを小さくすることで時間方向の解像度が良くなり，解の精度が向上します。それぞれの時間方向の離散化方法（差分スキーム）と計算精度について考えてみます。
熱伝導問題で現われる時間依存項は１階の時間微分項で，離散化は差分法で行なわれます。この１階の時間微分項の離散化について，時間方向の差分には次の３つのスキームがあります。 ○ 陽解法 ○ クランクニコルソン法（一般的な市販ソフトでデフォルトに採用） ○ 完全陰解法（一般的な市販ソフトでオプションに採用）まずはこれらの差分近似式を導出することを目的とします。
非定常熱伝導問題の微分方程式は次式で表されます。
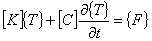
	（1）
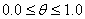
今，時間方向の刻み幅を dt [sec]，パラメータを θ とします。ここで， θ の値が取ることのできる範囲はです。 N ステップでの時刻を t_n とすると，時刻
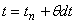
	（2）
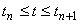
は，となります。
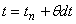
時刻における微分方程式は，添え字 n + θ を使用して次の式で表現されます。
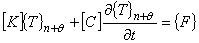
	（3）
ここで，時刻 t_n と t_n+1 の間における温度と時間の関係を線形近似すれば，以下に示す図のようになります。
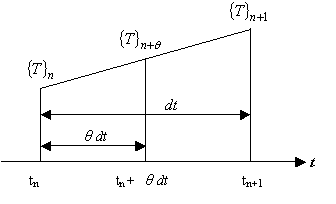
図1　時間と温度の関係
タイムステップ N + θ というものを仮想的に考えた場合，温度は次式で近似されます。導出方法はこちら
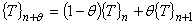
	（4）
またこのときの温度の時間変化率は次式で近似されます。
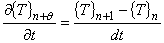
	（5）
（4）と（5）を（3）に代入します。
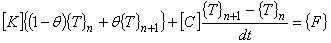
	（6）
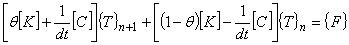
次のように整理します。それぞれの差分近似はこの式でパラメータ θ を決めることで得られます。
	（7）
θ = 0 のとき
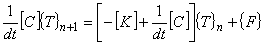
	（8）
θ = 1/2 のとき　（クランクニコルソンの陰解法）
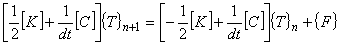
	（9）
θ = 1 のとき　（完全陰解法）
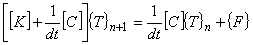
	（10）
以上で，時間方向の差分近似式がそろいました。今後はそれぞれの差分での計算を行い，検討を続ける予定です。