もう一度有限要素式を見てください。
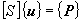
有限要素法では主に2つの代表的な境界条件があります。1つは第1種境界条件である固定境界条件(Dirichlet条件−ディリクレ条件)であり,もう1つは第2種境界条件である駆動境界条件(Neumann条件−ノイマン条件)です。
先に述べたように有限要素法は2階偏微分方程式を解くので未知数の一つ以上が既知として与えないと不定となって解くことができません。上の式では変位ベクトル{u}が最低でも1つは既知として与えなくてはならないということです。未知数を既知として与えるということは,どのような駆動(入力) にたいしても常に与えた値をとるつまり固定値をとるということになります。ですので一般に固定境界条件と言います。つまりこの条件は境界条件の中でも最も拘束度の高い条件であると言えます。
次に駆動ベクトル{P}が既知である場合があります。これは系を駆動する入力が既知である条件で,ノイマン条件に相当します。ノイマン条件でとくに{P}が0であるような場合については,自然境界条件と区別して呼んでいます。なぜなら有限要素法では、隣合う要素間における物理量の連続性を満たす条件が各要素間において自然に(自動的に)満たされるからです。隣合う要素がない境界に面した要素に何も境界条件を指定しない場合には自然境界条件が成り立つということです。 ただし個々のソフトウェアでの境界条件の設定についてはマニュアルを参照してください。ここではあくまで一般論で説明しています。