図 1 に示すように,媒質 1 と媒質 2 の境界上を電流密度 Js の表面電流が流れているものとします。
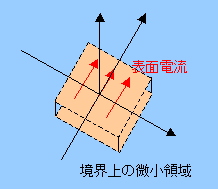
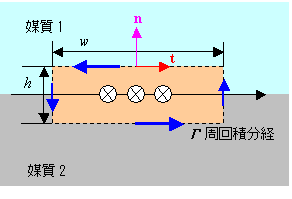
図 1 境界における磁場 2
境界面を面内方向に表面電流が流れているとすれば,当然その周囲には磁場 B [T] が生じます。
磁場 B [T] の境界条件に関して,ある閉領域中で磁場の湧き出しがないという条件,
すなわち磁場の連続性に関する条件を説明しました。
磁場ではこの発散ともうひとつ回転という大きな性質があります。
表面電流密度 Js を囲む断面を周回積分経路にとれば,
Ampereの法則により表面電流密度 Js が
周囲に作る磁場 B [T] との関係は次式のようになります。
微分形式:
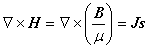
積分形式:
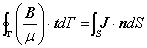
(1)
境界領域について,境界層の厚さ h を 0 に近づけていくと, 厚み方向の磁場の周回積分は 0 とみなすことができます。
すなわち,境界面に対して垂直方向の磁場の周回積分は無視できます。
したがって,境界層において上記の周回積分は,境界面の接線方向成分のみを考えればよいので, 次のようになります。
ここで,t は接線方向成分を意味します。

(2)
両辺を w で割ると,
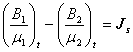
(3)
となります。
これが磁場の境界条件の回転という性質にかかわる部分です。
表面電流が存在しなければ,
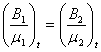
(4)
であり,媒質 1 と 2 において透磁率が異なる場合,
上式を満たすためには磁場 B の接線方向成分は等しくならないことが必要です。
以上より,「磁場 B の接線方向成分は境界では不連続になる」 という結論を得ます。



