マクスウェル応力法による電磁力の計算式は(1)で表されます。
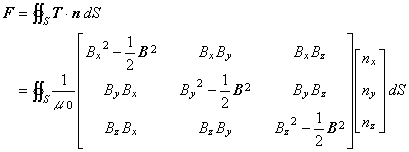
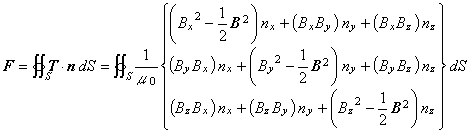
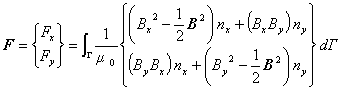
この式は,通常いろいろな参考書に登場しますが,その単位について調べてみましょう。
磁束密度の単位 = [T] = [ Wb / m2 ]
磁気透磁率の単位 = [ H / m ] = [ Wb / Am ]
積分路の長さの単位 = [ m ] 法線ベクトルの成分は無次元量です。
したがって, 式(2)の F の単位は,
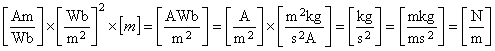
となり,単位長さあたりの力を表していることがわかります。
ここで単位長さとは,長さの単位を [ m ] としたので,1.0 [ m ] あたりということになります。
今計算は x - y 平面を仮定した 2 次元として扱っており,
そこから計算された力は, z 方向の次元の長さが欠落した量として求められます。
すなわち 2 次元問題で得られる力というのは,z 方向には単位長さあたりという仮定が伴っています。
そのため,実際の電磁力を求めるには,対称空間の z 方向の長さ Lz をかける必要があります。
(このことはほとんどの参考書では当たり前のこととして書かれていませんので要注意です)
2次元問題とは奥行き方向( z 方向 )に無限大の長さを仮定したモデルであるので,
そこで得られた磁場 B [T] というのはモデル化による誤差を伴っています。
さらに,そこから得られた磁場 B [T] をもとに電磁力を計算し,
そこには実物の奥行き方向の長さを与えるので,やはりモデル化誤差を含みます。
また,電磁力計算は,磁場 B [T] の 2 乗により計算するので,誤差も 2 乗で現われてくることに注意しましょう。
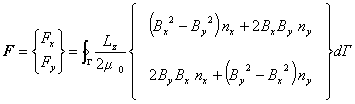
左図では,磁性体周辺を反時計回りに積分する様子が描かれています。
左図より 2 次元問題では,積分路のパターンは多くても 8 パターンしかないことがわかります。
法線ベクトルと x 軸とのなす角を θ とすると,図で法線ベクトルを描いた部分の積分路について考えれば, θ を調べることによりすべての経路に対応できます。
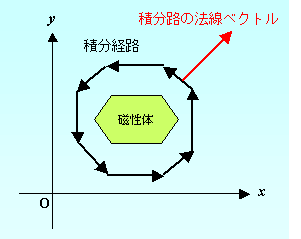
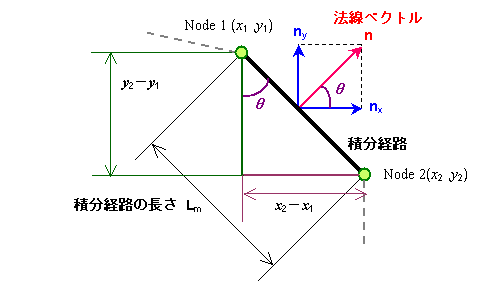
図 2次元問題の電磁力計算
積分路の一つに立てられた外向き法線 n の x 方向成分と y 方向成分の計算は,
右の図から次のようにして求めることができます。
法線ベクトル n が x 軸となす角を θ とすると法線ベクトル n の大きさが 1 であることより
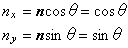
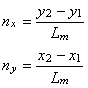
式(6)を式(4)に代入すれば 2 次元場の電磁力が計算できます。



