マクスウェル応力法による軸対称場の電磁力計算

マクスウェル応力法による軸対称場の電磁力計算
マクスウェル応力法による電磁力の計算式は（1）で表されます。軸対称場では，添え字を x ---> r y ---> θ z ---> z と読み替えればよいでしょう。
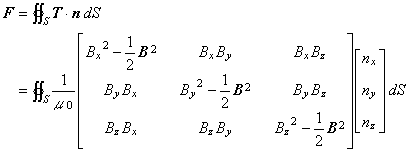
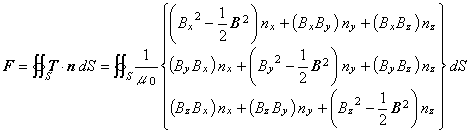
	（1）
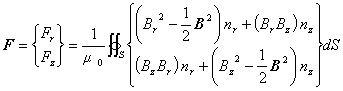
軸対称場では，式（1）で磁場 B [T] の θ 方向成分を 0 とおいた次式によって電磁力を計算します。
	（2）
この式は，通常いろいろな参考書に登場しますが，その単位について調べてみましょう。磁場 B の単位＝ [T] = [ Wb / m² ] 磁気透磁率の単位＝ [ H / m ] = [ Wb / Am ] 積分経路の面積の単位＝ [ m²] したがって，式（2）の F の単位は，[ N ] となり，2次元のときと異なり力の単位となります。
法線ベクトルの処理については，2次元問題のときと同様に下の図を考えます。
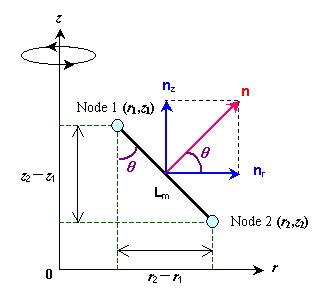
図１　軸対称場での積分要素の詳細
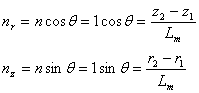
図１より，軸対称場では法線ベクトルの r , z 方向成分は次のように表されます。
	（3）
式(3)を式(2)に代入すれば次式が得られます。
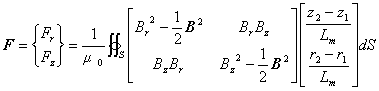
	（4）
軸対称問題では，計算モデルは 2 次元的な扱いですが，回転軸に関して対称であるというだけで，磁場の分布は 3 次元空間を意識しています。上の式ではマクスウェル応力と積分領域の面積との積の形をしています。積分領域については，積分路と r 軸とのなす角によって，次の図に示すように 3 つのパターンが存在します。なお，積分路の法線と r 軸とのなす角が正なのか負なのかを考える上で，積分経路を反時計回りに考えておくことが重要です。
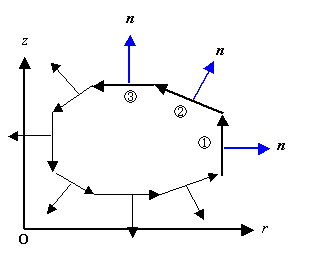
図2　積分経路は反時計回りになるように決めておきます。
上図の 3 つのパターンにより定義される領域は次の図のようになります。したがって，面積の計算方法は 3 つのパターンに対応しておく必要があります。
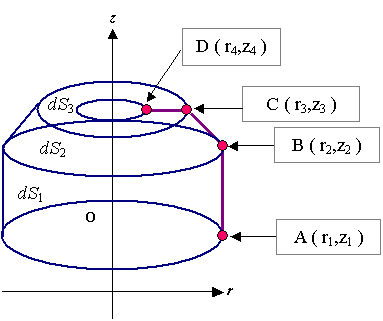
図3　積分経路が作る面の空間的な模式図（軸対称場では，計算は線要素に見えても物理的な扱いは面になることを忘れてはいけません)
（１）θ= 0　のとき
図 2 の１の部分は，法線ベクトルと r 軸が平行になるので，両者のなす角は 0 度になります。そして，図 3 に示すように 1 の積分領域の面積を dS₁ とすると，dS₁ は円筒部分の面積であるので
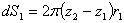
	（5）
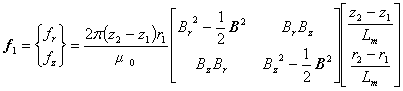
となります。したがってこの部分の電磁力を計算するときは次の式を使います。
	（6）
（2）θ = π / 2 のとき
図 2 の 3 の部分は，法線ベクトルと r 軸が直角になるので，両者のなす角は 90 度になります。そして，図 3 に示すように 3 の積分領域の面積を dS₃ とすると， dS₃ は円筒の底面部分の面積となりますので，
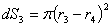
	（7）
であることは容易に理解できます。したがって，この部分の電磁力を計算するときは次の式を使います。
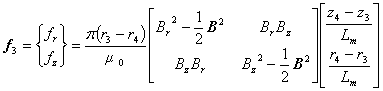
	（8）
（3）0 < θ < π / 2 のとき
このとき図 3 において点 D が回転軸（ z 軸）上に有る場合とそうでない場合に，場合分けされます。
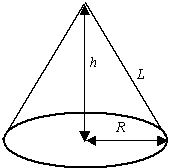
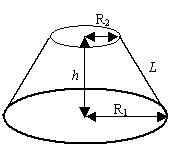
図 4　左：円錐の側面積について　　右：台形部分の側面積について（ L を母線といいます)
（3.1）D が回転軸上にある場合すなわち，r₄ = 0.0 のとき
dS₂は円錐の側面の面積になります。図 4 の左図を参考にすれば円錐の側面積は次の公式で表されます。
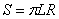
	(9)
公式に習って dS₂ を表現すると次式のようになります。
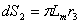
	(10)
したがって，この部分の電磁力を計算するときは次の式を使います。
	(11)
(3.2) 点 D が回転軸上にないとき，すなわち r₄ > 0.0 のとき
dS₂ は，図 4 の右図に示すように半径 R₁ と R₂，高さ h であるような直円錐円錐の側面積になります。この側面積は次の公式により求めることができます。
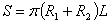
	(12)
公式に習って dS₂ を表現すると次式のようになります。
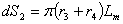
	(13)
ただし，
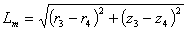
	(14)
です。
したがって，この部分の電磁力は以下の式で表されます。
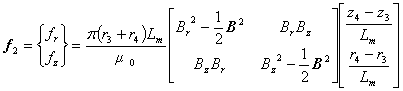
	(15)