ここでは,空間中に配置された永久磁石が周囲に作る磁場を解析します。
この解析の目的は,作成した解析プログラムの動作確認と精度検証にあります。
また,本問題は開領域問題といって磁場が無限遠方に広がる特徴があります。
しかしながら,有限要素法は領域型の解法のため,適当な領域で計算領域を打ち切らねばなりません。
打ち切ることでできる境界には境界条件を設定しますが,これはあくまで有限要素法を使用する人間側の都合でできる人工的な境界です。
このように人工的に定義される境界条件が計算結果に与える影響についても検討します。
なお,本問題は次の文献を参考にしています。
この文献は日本における磁場解析の黎明期に出版されたものですが,内容は簡潔にわかりやすくまとまっています。
研究室などに配属され,これから磁場解析を勉強する大学生の方は図書館などに行けばあるはずですのでしっかり勉強してください。
文献
加川幸雄:「電気・電子のための有限要素法の実際」,オーム社, pp.146-147
図1に物理的なモデルを示します。
x軸の正方向を磁化方向とする永久磁石が中央に置かれています。
永久磁石の寸法は,40[mm]×20[mm]です。
周囲の空気領域は永久磁石の中心を原点に考えて図に示すように3000[mm]×3000[mm]としています。
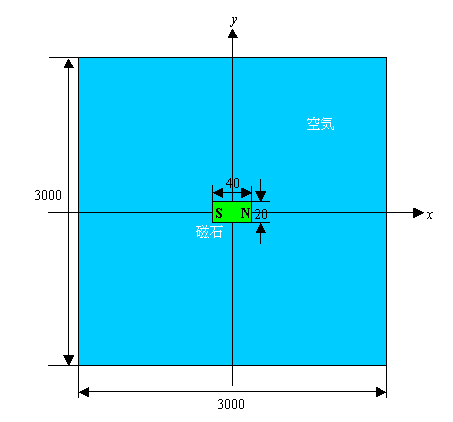
図1 物理モデル概要図
ここで,a はx方向の磁石の長さの2分の1,b はy方向の磁石の長さの2分の1を表すものとします。
2010年9月9日 以下のAzの式 の右辺3項目のlogの中括弧内に一部誤りがありましたので訂正します。
誤:(y+b)^2 正:(y-b)^2
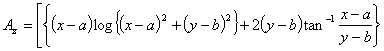
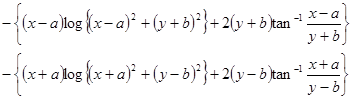
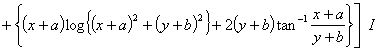
(1)
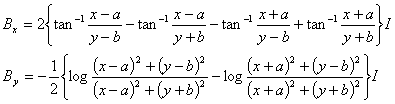
(2)
ただし,
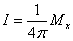
(3)
M は永久磁石の磁化で,本問題では0.38[T]とします。
(注意:ここでは,磁化を [T] の単位で定義されると考えています)
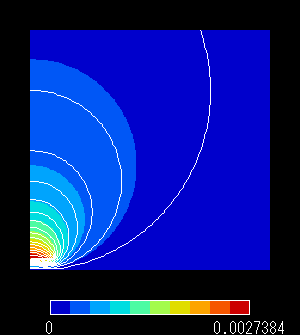
この式を計算して得られた,永久磁石がつくる磁場を図2に示します。
磁束線は原点に関して対称に分布しているのがわかります。
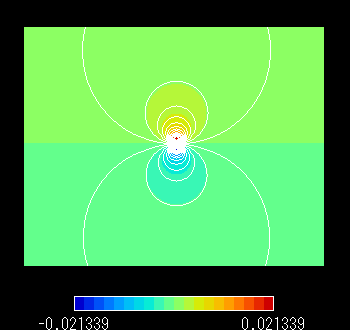
図2 永久磁石が作る磁場の理論解(ベクトルポテンシャル分布)
有限要素法による解析
解析モデル
次に,有限要素法による計算を行い,計算結果をこの理論解と比較することで計算精度や境界条件について検討します。
磁束線の分布は,原点に関して対称である事が上記の検討でわかったので,計算は第1象限のみを計算対象とする4分の1対称モデルで行います。
このように,物理現象の対称性を利用することで,モデルの規模を抑えた解析を行うことができます。
モデルの規模を抑えることで,計算時間と使用メモリー量を減らすことができます。
図3に計算モデルを示します。
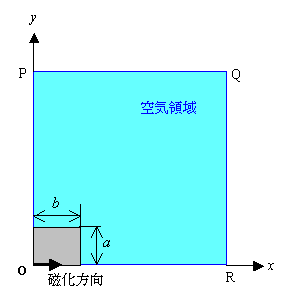
図3 計算モデル(4分の1対称モデル)
計算では空気領域は,
□ x方向について 200[mm] = 0.2[m]
□ y方向について 200[mm] = 0.2[m]
とします。
本当はもっと外側までの領域について計算領域を確保してもよいのですが,その分モデルの規模が大きくなります。
今回は検証を目的としているので,モデルの規模はなるべく小規模に押さえる方針とします。
磁石の寸法は,
□ a = 0.01[m]
□ b = 0.02[m]
です。
永久磁石の磁化方向は図に示すとおりで,その大きさは 0.38 [T] で一定とします。
図4に要素分割図を示します。
磁石付近は,1辺の長さが5[mm]程度になるように分割しています。
下のモデルの規模は,
節点数:484
要素数:882
です。
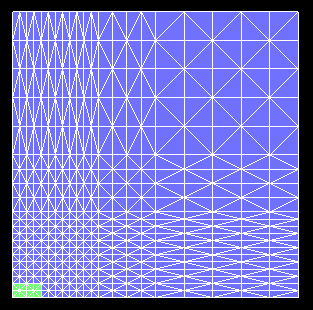
図4 要素分割図1
このメッシュで以下の計算を実行します。
この問題で特に注目すべきことは2点です。
それは, 境界条件の設定と要素サイズによる計算結果の変化です。
<境界条件>
計算モデルは4分の1対称モデルですので,
対称面(x軸上の節点とy軸上の節点)には,全体モデルでの物理現象を再現できる境界条件を導入します。
図2を見て下さい。
x軸上では磁束線が,軸と平行に分布しています。
これは磁石の磁化方向がx軸方向を向いているためです。
このように磁束線が境界に対して平行となるような場合は,ベクトルポテンシャルA = 0 とする固定境界条件を設定します。
次にy軸上の境界について見ます。
図2より,y軸上では磁束線が軸に対して垂直になっています。
このように磁束線が境界に対して垂直に分布する場合は,自然境界条件(磁場の接線成分が0,Ht=0)を設定します。
実際には,境界上に何も境界条件を設定しなければ,その境界は自然境界条件が設定されます。
有限要素法では,定式化の段階で自然境界条件を導入しているためです。
以上はモデルの対称性を考慮するための条件ですので正しく設定しなければ計算がうまくいきません。
次に残りの境界について考えます。
残りの境界は,有限要素法を利用することにより発生する人工的な境界です。
本来,このモデルの磁場は厳密には無限遠に広がるものです。
このような問題は,開領域型問題と呼ばれています。
有限要素法は,有限の領域を要素分割する解法であるため,現象が及ぶ無限の領域を要素分割することは不可能です。
そこで通常適当なところで解析領域を打ち切り,打ち切った境界上に境界条件を設定して問題を近似します。
なお有限要素法とは別に積分方程式法という解法があります。
積分方程式法 による解法では,場のポテンシャルを解析的に計算するため無限遠に広がる開領域問題で精度の高い解が期待できます。
電場,磁場,音場に代表されるように開領域型の問題を得意分野に持ちます。
有限要素法では,適当な領域で打ち切りますので,この境界に設定する条件としては次の3つが考えられます。
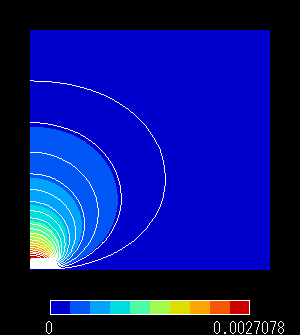
(1)固定境界条件 A = 0
この条件は,磁場は一般に距離の2乗で減衰すると考えられますので,注目領域より十分広い領域を取ればその境界では磁場を 0 と近似しても大過はないであろうという仮定により導入されます。
本来は磁場がわずかに残っている部分を強制的にA = 0 とするので,領域内では実際の現象より磁束密度の勾配が高くなります。
つまり理論解よりも,A は小さめに出力されます。比較的良く用いられますが,有限領域のサイズについて吟味する必要があるでしょう。
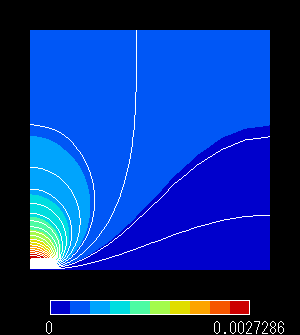
(2) 自然境界条件 Ht = 0
この条件は,磁場が有限領域と境界外部の領域について連続とするための条件です。
有限要素法は連続体を仮定した解法であるので,磁場が連続となるように解が選ばれます。
例えば,空気と磁性体では透磁率が異なるため磁性体に磁場が集中しその付近では複雑な分布をします。
しかしながら,磁場が空気と磁性体の境界で磁束線が途切れるということはありません。
磁場が途切れてしまうと,磁束密度の発散が0という条件が失われてしまうからです。
透磁率が等方的であるならば,境界上では磁場の接線方向成分を 0 とすればこの条件を満たすことができます。
実用上は,(1)と同様に注目領域より大き目の領域をとります。
この条件を設定すると,外部に透磁率の大きい磁性体で囲まれたのと同じ効果が発生しますので,境界を通過する磁束線が増加します。
したがって,理論解よりも A は大きめに出力されます。磁束線の分布は境界付近で異なった分布となります。したがって,有限領域のサイズについて吟味する必要があります。
(3) ハイブリッド型半無限要素の使用
有限要素法でも開領域問題を扱うために開発された要素です。有限領域の境界に設定することで,節点数や連立一次方程式方程式の元数を変更することなく,無限遠の効果を精度良く導入する事ができる要素です。これを使用すると磁場の分布は自然な形になります。
以上の3つの境界条件を使用して解析した結果について,
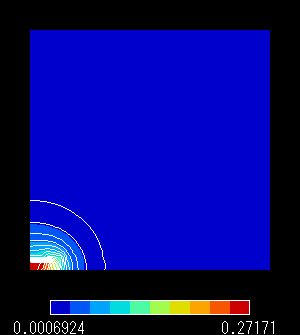
ベクトルポテンシャル分布を図5,6,7,8に示します。
磁束密度分布を図9,10,11,12に示します。
 |
 |
|
図5 ベクトルポテンシャル分布(理論解)
|
図6 ベクトルポテンシャル(固定境界条件)
|
 |
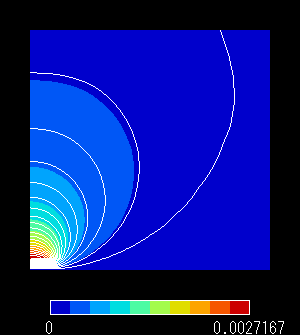 |
|
図7 ベクトルポテンシャル分布(自然境界条件)
|
図8 ベクトルポテンシャル分布(半無限要素)
|
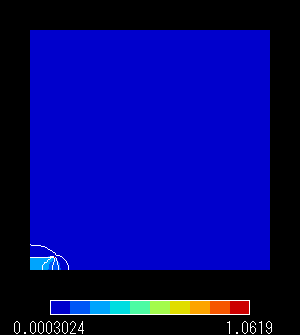 |
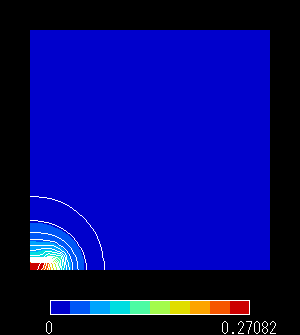 |
|
図9 磁束密度分布(理論解)
|
図10 磁束密度分布(固定境界条件)
|
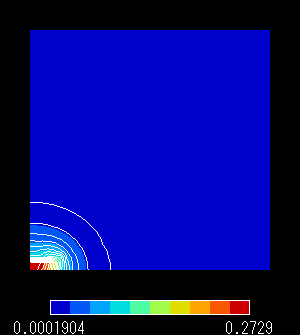 |
 |
|
図11 磁束密度分布(自然境界条件)
|
図12 磁束密度分布(半無限要素)
|
節点65 磁石内部 ---> 空気
節点68 磁石表面 ---> 磁石内部
節点90 磁石角部 ---> 磁石表面
表1 計算精度検証1(ベクトルポテンシャル)
|
節点番号
|
X座標
|
Y座標
|
媒質
|
理論解
|
固定境界条件
|
自然境界条件
|
半無限要素
|
|
24
|
0.005
|
0.005
|
磁石内部
|
0.0013236
|
0.0013049
|
0.0013154
|
0.0013095
|
|
47
|
0.010
|
0.010
|
磁石表面
|
0.0025699
|
0.0025277
|
0.0025485
|
0.0025367
|
|
49
|
0.010
|
0.020
|
空気
|
0.0017983
|
0.0017662
|
0.0018078
|
0.0017841
|
|
53
|
0.010
|
0.040
|
空気
|
0.0010882
|
0.0010432
|
0.0011265
|
0.0010790
|
|
61
|
0.010
|
0.100
|
空気
|
0.0004745
|
0.0003658
|
0.0005748
|
0.0004562
|
|
65
|
0.010
|
0.180
|
空気
|
0.0002672
|
0.0000584
|
0.0004504
|
0.0002247
|
|
68
|
0.015
|
0.005
|
磁石内部
|
0.0008660
|
0.0010627
|
0.0010731
|
0.0010671
|
|
90
|
0.020
|
0.005
|
磁石表面
|
0.0008025
|
0.0007958
|
0.0008062
|
0.0008003
|
|
91
|
0.020
|
0.010
|
空気
|
0.0016091
|
0.0015960
|
0.0016168
|
0.0016049
|
|
134
|
0.030
|
0.005
|
空気
|
0.0003434
|
0.0003499
|
0.0003603
|
0.0003543
|
|
137
|
0.030
|
0.005
|
空気
|
0.0008490
|
0.0008313
|
0.0008730
|
0.0008491
|
|
222
|
0.050
|
0.005
|
空気
|
0.0001074
|
0.0001043
|
0.0001147
|
0.0001087
|
|
229
|
0.050
|
0.040
|
空気
|
0.0004886
|
0.0004466
|
0.0005299
|
0.0004821
|
|
354
|
0.100
|
0.005
|
空気
|
0.0000249
|
0.0000197
|
0.0000304
|
0.0000241
|
|
369
|
0.100
|
0.100
|
空気
|
0.0002431
|
0.0001452
|
0.0003498
|
0.0002313
|
|
442
|
0.180
|
0.005
|
空気
|
0.0000075
|
0.0000020
|
0.0000152
|
0.0000067
|
|
461
|
0.180
|
0.180
|
空気
|
0.0001346
|
0.0000055
|
0.0003176
|
0.0001179
|
表2 計算精度検証1(ベクトルポテンシャルの誤差)
|
節点番号
|
X座標
|
Y座標
|
媒質
|
理論解 [%]
|
固定境界条件[%]
|
自然境界条件[%]
|
半無限要素[%]
|
|
24
|
0.005
|
0.005
|
磁石内部
|
0.0
|
-1.41
|
-0.62
|
-1.07
|
|
47
|
0.010
|
0.010
|
磁石表面
|
0.0
|
-1.64
|
-0.83
|
-1.29
|
|
49
|
0.010
|
0.020
|
空気
|
0.0
|
-1.79
|
0.53
|
-0.79
|
|
53
|
0.010
|
0.040
|
空気
|
0.0
|
-4.13
|
3.52
|
-0.84
|
|
61
|
0.010
|
0.100
|
空気
|
0.0
|
-22.91
|
21.14
|
-3.85
|
|
65
|
0.010
|
0.180
|
空気
|
0.0
|
-78.15
|
68.56
|
-15.90
|
|
68
|
0.015
|
0.005
|
磁石内部
|
0.0
|
22.71
|
23.91
|
23.23
|
|
90
|
0.020
|
0.005
|
磁石表面
|
0.0
|
-0.83
|
0.47
|
-0.28
|
|
91
|
0.020
|
0.010
|
空気
|
0.0
|
-0.82
|
0.48
|
-0.26
|
|
134
|
0.030
|
0.005
|
空気
|
0.0
|
1.88
|
4.92
|
3.18
|
|
137
|
0.030
|
0.005
|
空気
|
0.0
|
-2.08
|
2.82
|
0.02
|
|
222
|
0.050
|
0.005
|
空気
|
0.0
|
-2.91
|
6.81
|
1.22
|
|
229
|
0.050
|
0.040
|
空気
|
0.0
|
-8.61
|
8.44
|
-1.34
|
|
354
|
0.100
|
0.005
|
空気
|
0.0
|
-20.72
|
22.17
|
-3.05
|
|
369
|
0.100
|
0.100
|
空気
|
0.0
|
-40.29
|
43.89
|
-4.84
|
|
442
|
0.180
|
0.005
|
空気
|
0.0
|
-72.93
|
103.07
|
-11.07
|
|
461
|
0.180
|
0.180
|
空気
|
0.0
|
-95.95
|
135.96
|
-12.38
|
表3 計算精度検証1 (磁場 B [T])
|
節点番号
|
X座標
|
Y座標
|
媒質
|
理論解
|
固定境界条件
|
自然境界条件
|
半無限要素
|
|
24
|
0.005
|
0.005
|
磁石内部
|
0.2684621
|
0.2643938
|
0.26647509
|
0.2652867
|
|
47
|
0.010
|
0.010
|
磁石表面
|
0.1042257
|
0.0935334
|
0.09544481
|
0.0943528
|
|
49
|
0.010
|
0.020
|
空気
|
0.0581702
|
0.0631689
|
0.06135168
|
0.0623870
|
|
53
|
0.010
|
0.040
|
空気
|
0.0228534
|
0.0251391
|
0.02323142
|
0.0243140
|
|
61
|
0.010
|
0.100
|
空気
|
0.0045878
|
0.0056043
|
0.00351914
|
0.0046872
|
|
65
|
0.010
|
0.180
|
空気
|
0.0014684
|
0.0029927
|
0.00043972
|
0.0021223
|
|
68
|
0.015
|
0.005
|
磁石内部
|
0.2249771
|
0.2192468
|
0.22128629
|
0.2201212
|
|
90
|
0.020
|
0.005
|
磁石表面
|
0.1638313
|
0.1684212
|
0.17039622
|
0.1692674
|
|
91
|
0.020
|
0.010
|
空気
|
1.0619245
|
0.1169751
|
0.11815675
|
0.1174795
|
|
134
|
0.030
|
0.005
|
空気
|
0.0651942
|
0.0691189
|
0.07102698
|
0.0699343
|
|
137
|
0.030
|
0.005
|
空気
|
0.0215505
|
0.0403743
|
0.04065995
|
0.0404874
|
|
222
|
0.050
|
0.005
|
空気
|
0.0210819
|
0.0206355
|
0.02266387
|
0.0214973
|
|
229
|
0.050
|
0.040
|
空気
|
0.0061971
|
0.0118178
|
0.01210542
|
0.0119101
|
|
354
|
0.100
|
0.005
|
空気
|
0.0049519
|
0.0039410
|
0.00606363
|
0.0048141
|
|
369
|
0.100
|
0.100
|
空気
|
0.0012100
|
0.0023667
|
0.00233297
|
0.0022410
|
|
442
|
0.180
|
0.005
|
空気
|
0.0015042
|
0.0004179
|
0.00304156
|
0.0013377
|
|
461
|
0.180
|
0.180
|
空気
|
0.0003733
|
0.0003860
|
0.00038108
|
0.0007764
|
表4 計算精度検証1 (磁場Bの誤差)
|
節点番号
|
X座標
|
Y座標
|
媒質
|
理論解 [%]
|
固定境界条件[%]
|
自然境界条件[%]
|
半無限要素[%]
|
|
24
|
0.005
|
0.005
|
磁石内部
|
0.0
|
-1.52
|
0.74
|
1.18
|
|
47
|
0.010
|
0.010
|
磁石表面
|
0.0
|
-10.26
|
8.42
|
9.47
|
|
49
|
0.010
|
0.020
|
空気
|
0.0
|
8.59
|
-5.47
|
-7.25
|
|
53
|
0.010
|
0.040
|
空気
|
0.0
|
10.00
|
-1.65
|
-6.39
|
|
61
|
0.010
|
0.100
|
空気
|
0.0
|
22.16
|
23.29
|
-2.17
|
|
65
|
0.010
|
0.180
|
空気
|
0.0
|
103.80
|
70.05
|
-44.53
|
|
68
|
0.015
|
0.005
|
磁石内部
|
0.0
|
-2.55
|
1.64
|
2.16
|
|
90
|
0.020
|
0.005
|
磁石表面
|
0.0
|
2.80
|
-4.01
|
-3.32
|
|
91
|
0.020
|
0.010
|
空気
|
0.0
|
-88.98
|
88.87
|
88.94
|
|
134
|
0.030
|
0.005
|
空気
|
0.0
|
6.02
|
-8.95
|
-7.27
|
|
137
|
0.030
|
0.005
|
空気
|
0.0
|
87.35
|
-88.67
|
-87.87
|
|
222
|
0.050
|
0.005
|
空気
|
0.0
|
-2.12
|
-7.50
|
-1.97
|
|
229
|
0.050
|
0.040
|
空気
|
0.0
|
90.70
|
-95.34
|
-92.19
|
|
354
|
0.100
|
0.005
|
空気
|
0.0
|
-20.41
|
-22.45
|
2.78
|
|
369
|
0.100
|
0.100
|
空気
|
0.0
|
95.60
|
-92.81
|
-85.21
|
|
442
|
0.180
|
0.005
|
空気
|
0.0
|
-72.22
|
-102.20
|
11.07
|
|
461
|
0.180
|
0.180
|
空気
|
0.0
|
3.39
|
-2.08
|
-107.98
|
○表1,2,34より,遠方打ち切り境界に「固定境界条件」を設定した解析では,理論解と比較して計算解が低めに得られています。
○一方,「自然境界条件」を設定した解析では,計算解は高めに得られています。
○ハイブリッド型無限要素を使用すると全体的に誤差が他の条件より大きく減少することがわかります。
○磁場 B [T] 関しては,磁石付近ではどの条件を使用してもあまり差がないと言えそうです。
したがって,磁石付近の磁場分布に注目するならば,どの境界条件を使用するかというよりは,
「解析領域をどれだけ取るか」,「メッシュサイズをどうするか」ということのほうが鍵になると思われます。
計算領域を広く取れば,境界条件が注目部に及ぼす影響は相対的に軽減されることが予想されます。
メッシュサイズを小さくすれば,磁性体付近の磁場の変化を捉える精度が向上すると考えられます。
理論解では,永久磁石の角部に磁場の局所的な集中が表現されていますが,有限要素法による計算では3つの境界条件のいずれのケースでもこの現象を明瞭に捉えていません。このように角部は特異点といって,磁場が超越関数で変化することが知られています。
ここで使用した有限要素法は,ベクトルポテンシャルは節点間で1次近似であり,磁束密度は要素内で一定としています。
したがって,急激に変化するような場を解像度良く捉えるには要素サイズを非常に小さくしなければならないことが予想されます。
しかし実際の要素分割は大変手間がかかりますのでおのずと限界が出てきます。
したがって,このような特異点の磁場を精度良く捉えたい場合には,積分方程式法に軍配が上がるでしょう。
積分方程式法にはいろいろな種類のものがあります。
例えば,境界要素法は,線形解析ではその有効性が報告されていますが非線形解析や多連結型の領域問題になると複雑になり長所が薄れてしまいます。 なによりも定式化の難易度が有限要素法に比べて相当高くなります。
今後の発展としては,次のようなものが考えられます。
(1) メッシュのパターンを変えた場合
(2) メッシュのサイズを変えた場合
(3) 解析領域を変えた場合
この問題は非常に簡単なセットアップで行なうことができますので,これから磁場解析(磁界解析)を行うという人は,ぜひ実習してみてください。
本番では難しいことをやるとしても,このような基本的な計算により
○ 有限要素法で得られる解がメッシュに依存すること
○ 境界条件により計算結果が影響を受けること
○ 対称性を利用したモデルの省略方法
といった最低限の知識を学ぶことができます。
そして,このような実習結果は,やりっぱなしにしないで必ず文書にして何をやり何を学んだかをまとめておいてください。
後日後輩に説明するときにも役に立つでしょうし,経験を積んで何年か経った時には良い思い出の品になると思うからです。