2 次元磁場解析 No.8 / Newton-Raphson 法による非線形解法
　前に説明したように磁気抵抗率 ν [m/H] と 磁化 M [T] といった磁気特性が含まれています。
これらは，磁場 B [T] の関数です。
そして，磁場 B [T] は，磁気ベクトルポテンシャル A [ Wb / m2 ] の関数です。
解析領域に強磁性体などのような非線形な磁気特性を持った媒質が存在する場合には， 有限要素式が A に関する非線形方程式となるため，区分線形近似による反復解法によって 解を求めなくてはなりません。これには，一般的に Newton-Raphson 法を用います。
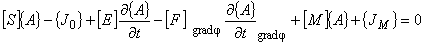
No.7では，２次元磁場・磁界解析の有限要素式が次式で表されることを説明しました。
（8.1）
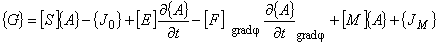
Newton-Raphson法を念頭に入れて，ベクトル {G} を次のように定義することにします。
（8.2）
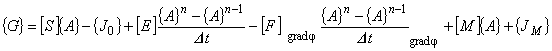
時間微分項を１階の後退差分近似を用いて表すと次式のように表されます。
（8.3）
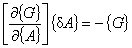
ここで，Newton-Raphson法による非線形方程式は次式で定義されます。
（8.4）
ニュートン･ラプソン法では，A の初期値を適当に仮定してから，式（8.4）の非線形方程式を解いて， ベクトルポテンシャル A の増分値 δA を求めます。なお A の初期値は，1 ステップ目において通常 0 とします。
得られた増分値を用いて，次の式より新しい A を求めます。 この過程を A の変化が収束するまで繰り返します。
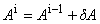
（8.5）
ここで，肩の添え字 i は，ニュートン･ラプソン法の反復回数を示します。
A の収束判定値は解析者が決定します。
収束条件が緩すぎると，A の精度が落ちます。
磁場解析では多くの物理量が A の影響を受けるので，ある程度正しい A が求められないと 解析結果がおかしくなります。
一方で，収束条件を厳しくし過ぎると，今度は 1 ステップあたりの収束に要する計算時間が増加するため， トータルの解析時間が極端に長くなることがあります。
したがって，Newton−Raphson法の収束判定値は，事前に検討して妥当性とコストのバランスを確認しておくようにします。
一般的には，1.0E-03〜1.0E-04 程度で十分です。 		　
ところで，ニュートン･ラプソン法による非線形方程式を解くためには， 有限要素式のベクトル {G}と，感度行列 [d{G}/d{A}] を求めておかねばなりません。
ここで，2 つの列ベクトル
　　
によって定義される感度行列は次の式で定義されます。
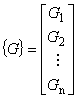
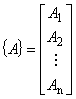
(8.6)
感度行列の計算について説明します。
{G} を {A} で偏微分すると次の式が得られます。
{G} に含まれる磁気抵抗率 ν [m/H]，磁化 M [T] は，磁場 B [T] の関数であるので， これらは磁気ベクトルポテンシャル {A} の関数となっており偏微分の際にはこれらに注意して下さい。
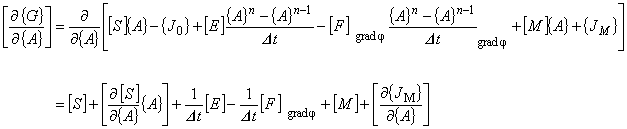
（8.7）
ここで，[S],[E],[F],[M] といったマトリックスは No.7 で説明しました。
ここでは，式（8.7）の右辺第 2 項，右辺第 6 項について説明します。
[S]{A} という列ベクトルを，{A} という列ベクトルによって偏微分するのであることから次式が得られます。
直交異方性を仮定した表現 / [(d[S]/d{A}){A}] マトリックスの導出 /
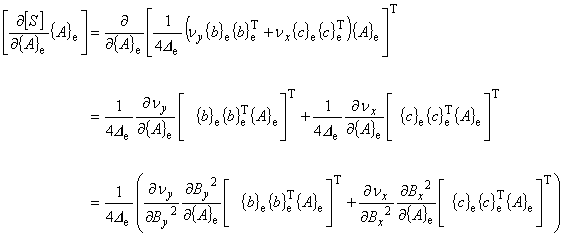
（8.8）
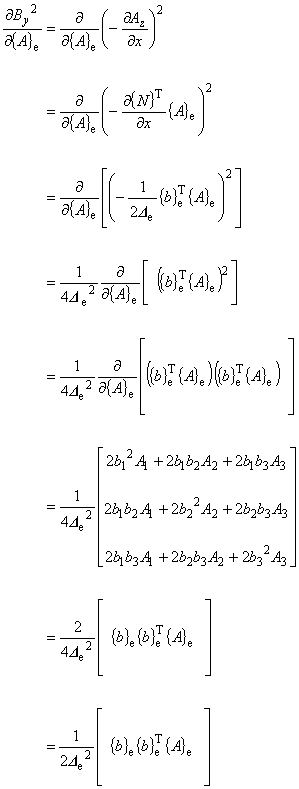
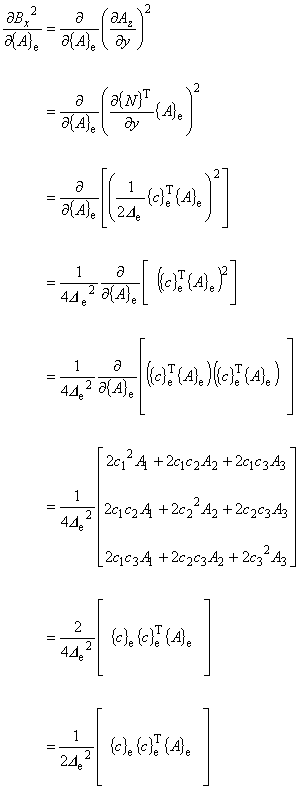
ここで，磁気抵抗率 ν は，本来磁場 B の関数ですが，磁場 B の 2 乗である B2 の関数としています。磁気抵抗率を磁場 B の2乗で偏微分する項のデータは入力データで与えた B-Hカーブより算出します。
　　　
（8.9）
式（8.9）を式（8.8）に代入すれば
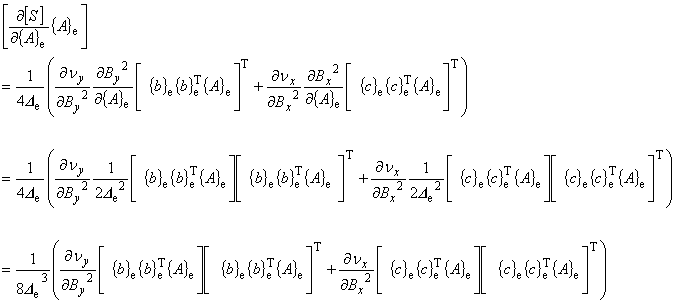
（8.10）
を得ます。
等方性を仮定した表現 / [(d[S]/d{A}){A}] マトリックスの導出 /
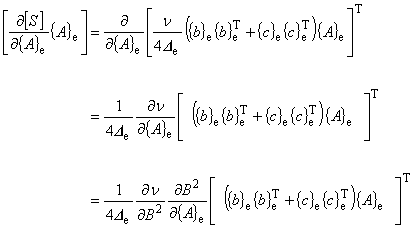
（8.11）
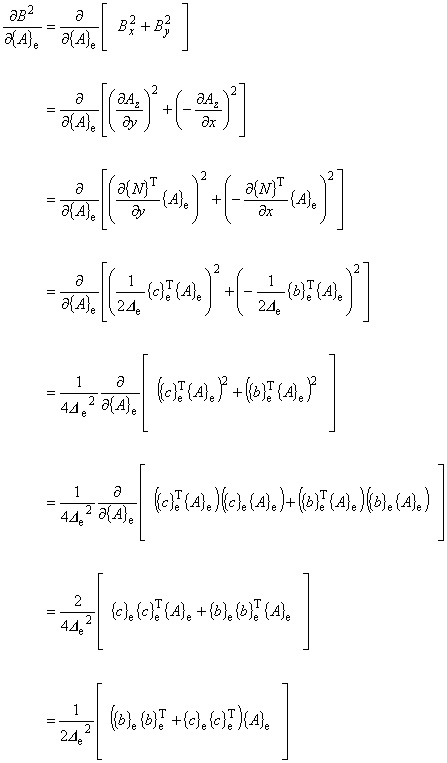
（8.12）
式（8.12）を式（8.11）に代入すれば
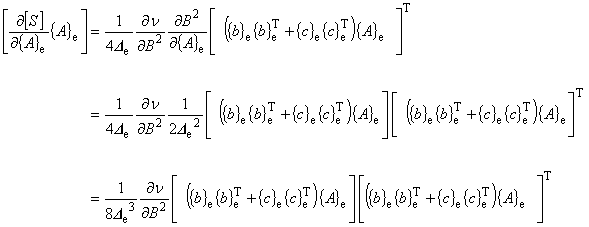
（8.13）
を得ます。
直交異方性を仮定した表現 / [d{JM}/d{A}] マトリックスの導出 /
等価磁化電流密度の非線形項について説明します。
まず，磁化 M [T] の直交異方性を考慮した場合の表現は次のようになります。
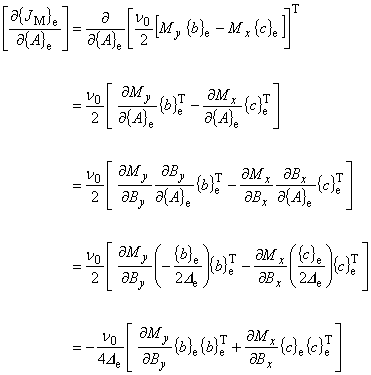
（8.14）
磁化方向の任意性を仮定した表現 / [d{JM}/d{A}] マトリックスの導出 /
磁化方向を任意とした場合は次のように考えます。
この場合，磁化 Md [T] は，磁化と同じ方向の磁場 Bd で偏微分しなくてはなりません。
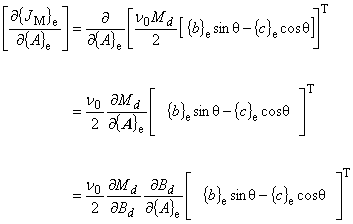
（8.15）
ここで，Bd は次の式で表されます。
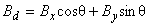
（8.16）
三角形 1 次要素の場合は，次のように成分表示できます。
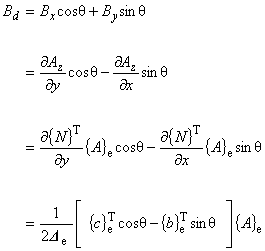
（8.17）
これを式（8.15）に代入すれば次の式が導出されます。
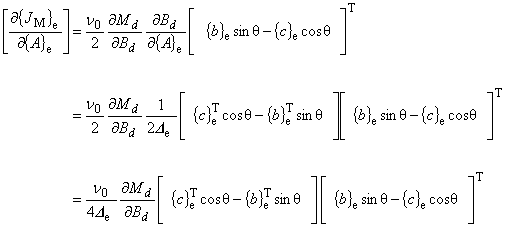
（8.18）
以上より，Newton-Raphson法の非線形方程式を解くために必要な各項の成分が明らかになりました。
これで２次元磁場・磁界解析の説明を終わります。