今回は，軸方向の長さが無限にあるソレノイドコイル内の磁場解析を行います。
この問題は，電磁気学や電気工学の教科書に必ず出ている古典的な問題です。
次のように理論解が与えられます。

単位長さあたりのコイルの巻き数を n [1/m] とし，
真空の透磁率をμ0 [H/m]，
コイルに流れる電流値をI [A]とすると，
コイル内の磁束密度 B [T] は次式で表されるように一様になります。

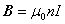
磁場はソレノイドコイル内に一様となり，コイルの外部では磁場は0となります。

今回，次の文献を参考に問題を無端ソレノイドの問題を作り解析を行いました。
解析の目的としては，解析プログラムの動作確認と，
このような古典的な問題を有限要素法で解くとどのような結果になるかを知ることです。

文献 中田高義，高橋則雄：「電気工学の有限要素法」森北出版，p.77

＜計算モデル＞
図１に計算モデルを示します。 図１に示す寸法はすべて[mm]です。
z軸方向をソレノイドの軸方向とし，軸対称問題として取り扱います。
z方向の長さは無限に長いのでこの方向の長さは自由に設定することができます。
コイルの断面積S[m2]は

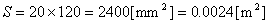
とし，コイルに流れる電流は直流電流とし，400 [A]を設定しました。
図2に要素分割図を示します。
計算モデルの規模は
節点数：565
要素数：896

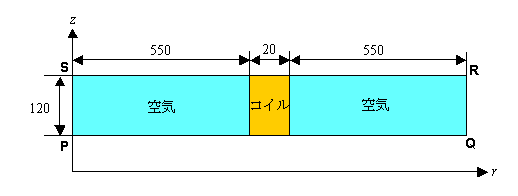
図１　無端ソレノイドの計算モデル

図2　無端ソレノイド要素分割図

＜境界条件＞

　軸対称解析なので，回転軸であるPSは自動的にA = 0 [Tm]が設定されます。
　次に他の境界について考えてみます。
　軸方向すなわち z 方向については無限に長いので物理量の出入りは境界上でプラスマイナス0としてよく，磁場解析ではこれは自然境界条件に相当します。したがって，PQおよびRSの境界には自然境界条件を設定します。
　次にソレノイドコイル外部の空気領域上にある境界QRについて考えます。
　遠方領域を打ち切ることで生じる境界であるので，空気領域を十分広く取った上でベクトルポテンシャルA = 0 を課すのが一般的です。
　 しかしこの考えを無端ソレノイドコイル問題に適用すると，コイルの外部にベクトルポテンシャルの分布が誘導されるために，本来あるはずの無い磁場が生じ，おかしな解が得られることがわかっています。
　 したがって，遠方打ち切り境界に適用できる条件として自然境界条件を設定します。
　

計算結果を図3,4,5に示します。

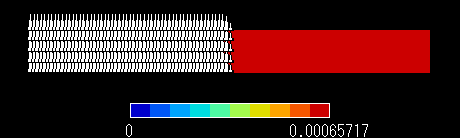
図3　計算結果　ベクトルポテンシャル１

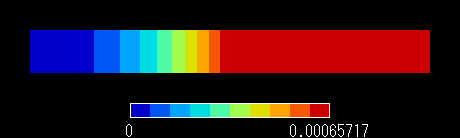
図4　計算結果　ベクトルポテンシャル分布

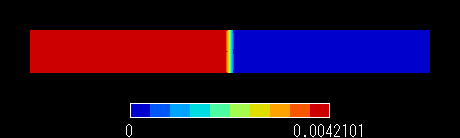
図5　計算結果　磁束密度分布

　図5より，磁場がコイル内にのみ存在していることがわかります。
　またコイル内の磁束密度は，電磁気学の教科書で説明されているように一様となっています。
　コイル内の磁束密度は 0.0042[T]という結果になりました。

　ここでは，計算で得られた値 0.0042[T]を電磁気学の理論解と比較することを考えます。
　しかしながら，すぐに困ったことに気がつきます。
　それは巻き数 n の取り扱いと解析でのコイル領域の設定の仕方です。
　解析では巻き数などのことは考えずに適当にコイル領域を決めて計算しました。
　しかし，計算した後で電磁気学の式の答えと比較しようとすると巻き数 n が存在するのでうまくできません。
　 ソレノイドコイルの一般的な基本構造は下図のようになっています。

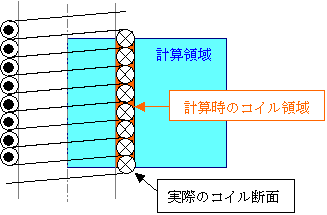
図6　ソレノイドコイル断面図

　電磁気学では，コイルの巻き数 n を要求されます。
　例えば上の図では n = 7 です。
　計算では，コイルを矩形断面で表現したので，電磁気学で考えているコイル断面よりも大きく考慮されていることになります。
　したがって，このままでは電流値を理論解と有限要素法で同じとした場合，計算結果は合いません。

　計算ではコイルの断面積は図1より，0.02 [m]×0.12[m]としたのでこれはそのままにします。
　「実際のコイルの半径を 0.01 [m]と考えれば」，コイル1巻きあたりの断面積は

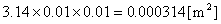
となるので，計算で設定したコイル断面積には

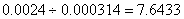
個のコイルが存在することになります。
これを用いて理論の式 B = μ0 n I に代入します。

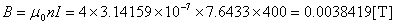
となり，計算結果に対して約10%程度小さい結果となりました。

今度は，計算結果より得られたコイル内の磁束密度から逆にnを理論式より求めると次のようになります。

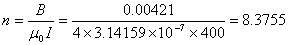
結果がなぜこのように異なるかを考えてみることは面白いかもしれません。

ここまでのプロセスをまとめると次のようになります。

（１）計算モデルは適当にコイル断面を矩形領域で定義しました。
（２）計算により得られた磁束密度が正しいかを検討するために理論式を当たってみました。
理論解を求めるために，
（３）コイルの断面を円形断面と仮定し1巻きあたりの断面積を求めました。
（４）解析で設定した矩形断面積を先に求めたコイル1巻きの断面積で割ってnを求めました。
（５）この n を用いて理論式より磁束密度を求めました。
（６）計算より得られた磁束密度を理論式に代入して n を求めました。
計算結果と理論式で磁束密度が合いませんでした。

コイル断面積の考え方に問題がある？
電磁気学の理論式がこの計算モデルの答えを比べるのに適しているかどうか？
プログラムに問題がある？
動作確認をしようと思っていたのですがなかなかうまくいかないものです。
コイルの巻き数は層数が増えれば変わりますし，等価な断面にしてモデリングしている場合は一度無端ソレノイドモデルを作って試してみはいかがでしょうか？

「おまけ」

計算結果からわかると思いますが，磁場はコイル内にのみ存在しています。
したがって，計算ではソレノイド外部の空気領域を考慮する必要はありません。
コイルの端を境界とし，そこに自然境界条件を課せば十分であす。
ところで，境界条件のところで述べたように解析では境界RQに A = 0 を課すとおかしな結果になります。
RQに自然境界条件ではなく固定境界条件 A = 0 を課した場合の結果を図7,8,9に示します。

図７　誤った計算結果（ベクトルポテンシャル分布)

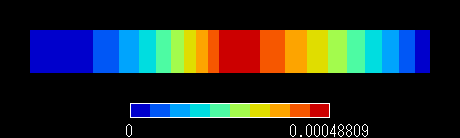
図8　誤った計算結果（ベクトルポテンシャル分布）

図9　誤った計算結果（磁束密度分布）