磁場解析 例題4 軸対称コイルの周囲に作られる磁場
2003/12/30 更新
今回は,軸対称コイルの周囲に作られる磁場を解析します。
本問題は,下記の文献を参考に作成しました。
この問題の結果は文献にグラフの形で掲載されていますので,作成したプログラムの動作確認や精度の検証にも使えます。
文献では,境界要素法によって得られた磁束分布が掲載されており,有限要素法では境界条件のため磁束線が境界付近で現実と異なる分布になるのに対してきれいな分布となっています。なお下記文献は渦電流gradφなどについても丁寧に記述されており良書だと思います。
文献
加川幸雄,榎園正人,武田毅:日本シミュレーション学会編計算電気・電子工学シリーズ1「電気・電子境界要素法」,森北出版,p.128-136
本問題は軸対称静磁場問題であり,その計算モデルを図1に示します。
文献では,コイルの内側を鉄心とした場合と空気とした場合について解析しています。
計算データとしては,鉄心部は空気部のドメインを分けて作成しておきます。
そうすれば,材料定義のところで鉄心と空気を交換するだけでメッシュを作成しなおす手間が省けて楽です。
メッシュ図を図2に示します。
メッシュのサイズは5[mm]とし,解析領域を図1の右図のように変更して解析します。
メッシュサイズは同じにしたままで,解析領域を変更しますので,計算結果を比較すると計算領域が結果に及ぼす影響を知ることができます。
計算結果の評価は,コイル中央部より z 方向に 0.015[m]のところから0.100[m]までの領域についての磁束密度で行います。
<計算領域>
解析領域 小 : 縦 0.08[m] ×横 0.16 [m]
解析領域 中 : 縦 0.32[m] ×横 0.22 [m]
解析領域 大 : 縦 0.80[m] ×横 0.42 [m]
<コイルの電流>
コイルには直流電流を定義し,電流密度 J = 1.0E+06 [A/m2] を与えます。
<鉄心>
鉄心の比透磁率は20000です。
<境界条件>
軸対称問題ですから,回転軸である境界 ad には,ベクトルポテンシャルA = 0 [ Wb m ] を課します。
残りの境界は,自然境界条件を設定します。
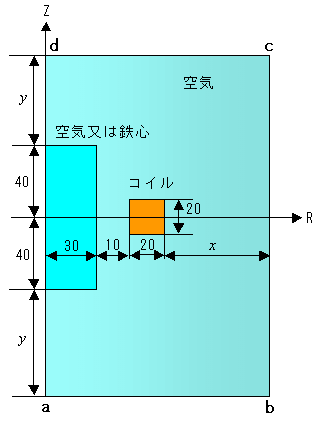
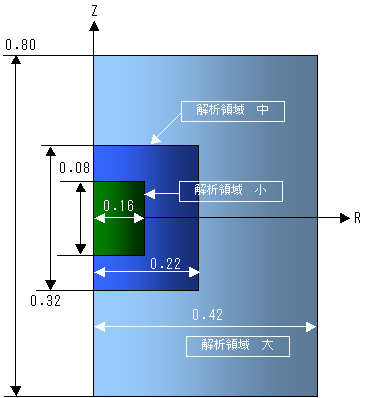
図1 モデル概要図
(左図の長さの単位はミリです)
(右図の長さの単位はメートルです)


図2 メッシュ図 左:空芯コイル 右:鉄心コイル
また解析領域が結果に及ぼす影響を調べるため,磁束密度による比較を図6に示します。
表1に,図6に示したグラフの数値を掲載します。
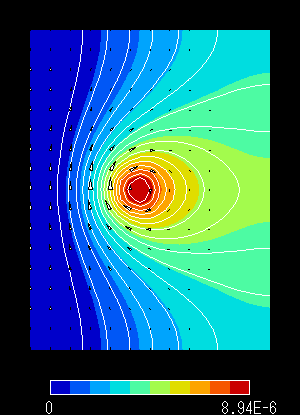
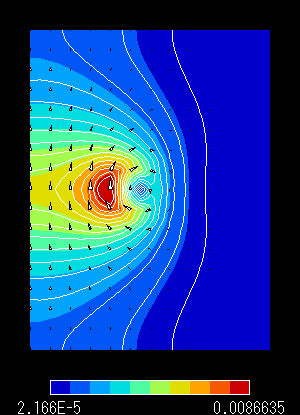
図3 解析領域 「小」 での結果
左:磁束線分布 右:磁束密度分布
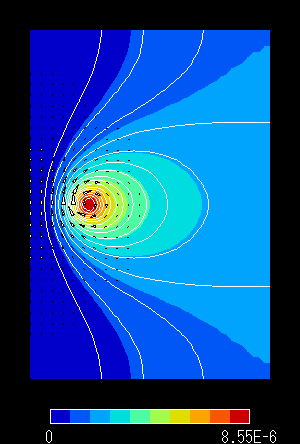
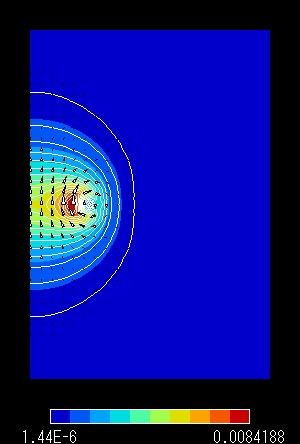
図4 解析領域 「中」 での結果
左:磁束線分布 右:磁束密度分布
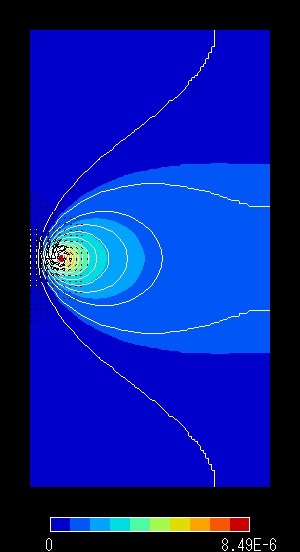
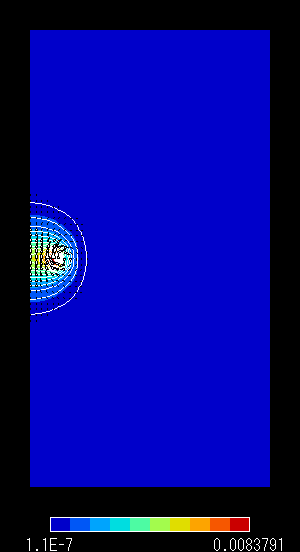
図5 解析領域 「大」 での結果
左:磁束線分布 右:磁束密度分布
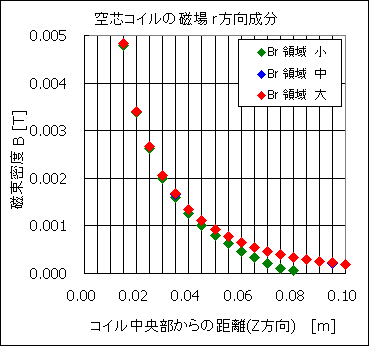
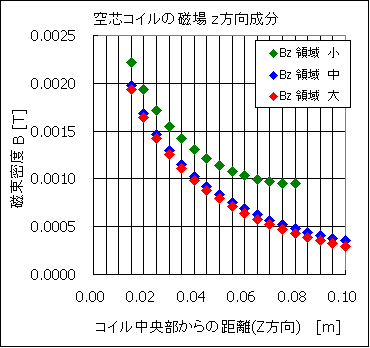
図6 磁場Bの比較(解析領域による影響)
表1 磁束密度による比較 (r = 0.05,z = 0.015 --->
0.100 の点で測定)
(節点での磁場Bの値は,要素の磁場Bを単純平均して算出してあります)
|
解析領域 小
|
解析領域 中
|
解析領域 大
|
||||
|
z 座標
|
Br [T]
|
Bz[T]
|
Br [T]
|
Bz [T]
|
Br [T]
|
Bz [T]
|
|
0.015
|
0.004799
|
0.002221
|
0.004826
|
0.001977
|
0.004827
|
0.001936
|
|
0.020
|
0.003374
|
0.001930
|
0.003411
|
0.001682
|
0.003413
|
0.001641
|
|
0.025
|
0.002622
|
0.001720
|
0.002670
|
0.001467
|
0.002672
|
0.001426
|
|
0.030
|
0.001997
|
0.001553
|
0.002056
|
0.001292
|
0.002059
|
0.001250
|
|
0.035
|
0.001596
|
0.001420
|
0.001670
|
0.001151
|
0.001673
|
0.001109
|
|
0.040
|
0.001253
|
0.001309
|
0.001342
|
0.001029
|
0.001346
|
0.000986
|
|
0.045
|
0.001007
|
0.001217
|
0.001113
|
0.000926
|
0.001118
|
0.000882
|
|
0.050
|
0.000790
|
0.001142
|
0.000917
|
0.000835
|
0.000922
|
0.000790
|
|
0.055
|
0.000621
|
0.001080
|
0.000771
|
0.000755
|
0.000777
|
0.000710
|
|
0.060
|
0.000468
|
0.001032
|
0.000645
|
0.000686
|
0.000651
|
0.000639
|
|
0.065
|
0.000339
|
0.000994
|
0.000548
|
0.000624
|
0.000555
|
0.000576
|
|
0.070
|
0.000218
|
0.000968
|
0.000462
|
0.000570
|
0.000470
|
0.000520
|
|
0.075
|
0.000108
|
0.000952
|
0.000396
|
0.000521
|
0.000405
|
0.000470
|
|
0.080
|
0.000053
|
0.000948
|
0.000336
|
0.000479
|
0.000346
|
0.000426
|
|
0.085
|
0.000289
|
0.000441
|
0.000300
|
0.000387
|
||
|
0.090
|
0.000247
|
0.000408
|
0.000259
|
0.000352
|
||
|
0.095
|
0.000213
|
0.000379
|
0.000226
|
0.000320
|
||
|
0.100
|
0.000182
|
0.000353
|
0.000196
|
0.000292
|
||
計算結果より,磁場の注目領域(このような問題ではコイル周辺など)に対して,計算領域が小さいと境界条件の影響で解の精度が低下することがわかります。
有限要素法では,遠方領域を打ち切った場合の境界条件としては自然境界条件がよく利用されます。
本問題でも,打ち切りのための境界条件として自然境界条件をしています。
このように,開領域問題を打ち切って領域を設定する場合には,解析領域を注目領域に対して大きめに取る必要があることを示しています。
本問題では,解析領域を中とした場合と大とした場合でさほど結果が変わっていないので,中程度の領域を確保することが大事だと思われます。
また,計算結果を見る限り作成したプログラムは正常に動作していると考えてよさそうです。
なお,無限要素を使用すれば,状況は改善されると思われます。
磁場解析を行う場合は,このように領域を変更してみて設定している領域が計算結果へどの程度,影響しているかを知ることは重要です。
実際には,時間がとれないことも多くなかなかそこまでできませんが,このような簡単な問題でよいので,一度は自身の手で確かめておくことが非常に大切です。
今後の展開としては,鉄心を使用した場合が考えられます。
境界条件による比較
2003/12/30 追加
(1)ポテンシャル A = 0
(2)自然境界条件
(3)半無限要素
として結果を比較してみます。境界条件以外の計算条件はすべて上記と同じです。
結果 コンター図
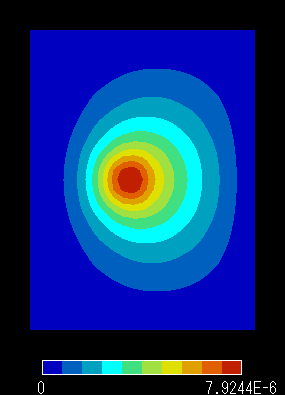 |
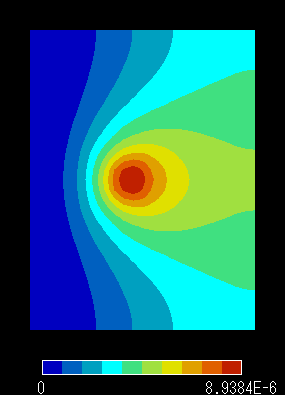 |
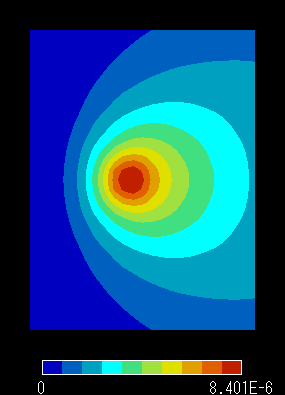 |
|
磁束線図 (固定境界条件) |
磁束線図 (自然境界条件) |
磁束線図 (半無限要素条件) |
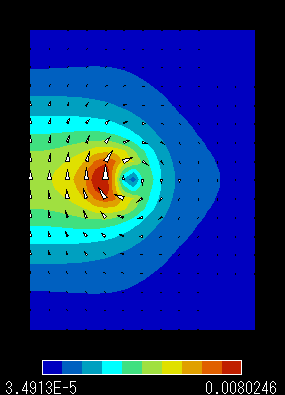 |
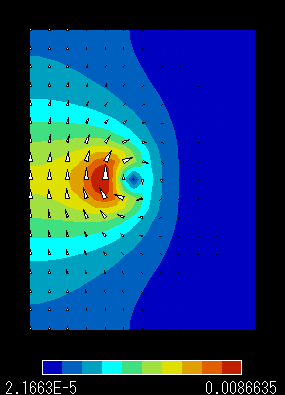 |
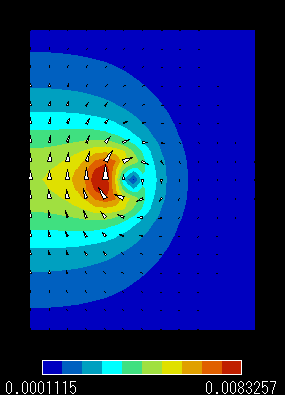 |
|
磁場B分布 (固定境界条件) |
磁場B分布 (自然境界条件) |
磁場B分布 (半無限要素条件) |
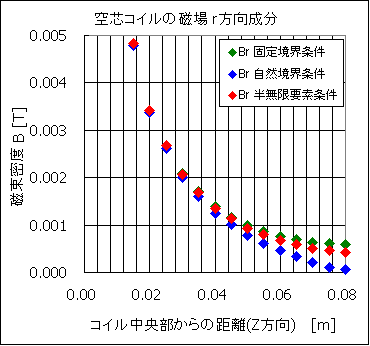
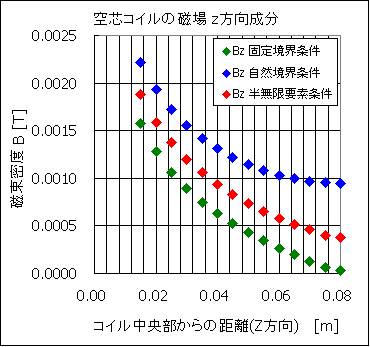
磁場Bの比較(境界条件による影響)
表2 磁場Bによる比較 (r = 0.05,z = 0.015 --->
0.100 の点で測定)
(節点での磁場Bの値は,要素の磁場Bを単純平均して算出してあります)
|
固定境界条件
|
自然境界条件
|
半無限要素
|
||||
|
z 座標
|
Br [T]
|
Bz[T]
|
Br [T]
|
Bz [T]
|
Br [T]
|
Bz [T]
|
|
0.015
|
0.004834
|
0.001572
|
0.004799
|
0.002221
|
0.004829
|
0.001882
|
|
0.020
|
0.003422
|
0.001278
|
0.003374
|
0.001930
|
0.003414
|
0.001587
|
|
0.025
|
0.002687
|
0.001064
|
0.002622
|
0.001720
|
0.002675
|
0.001372
|
|
0.030
|
0.002079
|
0.000890
|
0.001997
|
0.001553
|
0.002063
|
0.001197
|
|
0.035
|
0.001700
|
0.000748
|
0.001596
|
0.001420
|
0.001679
|
0.001056
|
|
0.040
|
0.001383
|
0.000626
|
0.001253
|
0.001309
|
0.001354
|
0.000933
|
|
0.045
|
0.001167
|
0.000520
|
0.001007
|
0.001217
|
0.001129
|
0.000829
|
|
0.050
|
0.000985
|
0.000426
|
0.000790
|
0.001142
|
0.000937
|
0.000736
|
|
0.055
|
0.000860
|
0.000342
|
0.000621
|
0.001080
|
0.000797
|
0.000655
|
|
0.060
|
0.000755
|
0.000265
|
0.000468
|
0.001032
|
0.000677
|
0.000582
|
|
0.065
|
0.000687
|
0.000194
|
0.000339
|
0.000994
|
0.000588
|
0.000517
|
|
0.070
|
0.000634
|
0.000127
|
0.000218
|
0.000968
|
0.000511
|
0.000457
|
|
0.075
|
0.000608
|
0.000063
|
0.000108
|
0.000952
|
0.000456
|
0.000402
|
|
0.080
|
0.000596
|
0.000031
|
0.000053
|
0.000948
|
0.000429
|
0.000376
|
軸対称問題における,境界条件による磁場の影響を比較検討しました。
磁場は無限遠方に分布していますが,有限要素法では有限領域における解析となるため,注目領域より少し離れた部分に境界を設けて解析領域を打ち切る必要があります。
この人工的な境界に,境界条件を設定する必要があります。
磁気ベクトルポテンシャル A = 0 とする固定境界条件では,実際には磁場が無限遠方に分布するため人工的な境界で Aの絶対値は 0 より大きくなります。
そのため,固定境界条件を設定した場合,磁場は低めに見積もられることが直感的にわかると思います。
自然境界条件では,人工的な境界の外部の媒質情報が未知であり,あらゆる媒質との連続性を満たすことを想定しています。これは境界外部に,磁性体が存在するような状況であり,磁場は境界へ集中しようとします。そのため,自然境界条件では実際の磁場よりも高く見積もられることが直感的にわかるかと思います。
無限要素条件では,有限要素に遠方場でポテンシャルが0に減衰するような補間関数が用いられ人工的な境界における磁場は上記の2つの条件より,実際の解に近づきます。つまり精度が向上します。このことは,注目部位のメッシュ数が増加して計算機のリソースを消耗するような場合,解析領域を小さくして無限要素を併用することで計算が可能になるケースがあることを示唆しています。
以上より,次のことが言えそうです。
自然境界条件での計算結果 > 無限要素条件での計算結果,実際の結果 > A = 0 の固定境界条件での計算結果
みなさんも,御自分のテーマとしている問題で上記のことを確認してみてはいかがでしょうか。