例題 10　速度効果を考慮した２次元定常磁場解析
磁場の中を導電性を有する物体が移動すると，物体に渦電流が誘起されこの渦電流により新たな抵抗磁場が誘起されます。 この効果を速度効果と呼ぶことにします。 今回は次の文献を参照して速度効果を考慮した２次元定常磁場解析を行なってみました。

出典
伊藤元哉，織田村元視，萩原修哉，大野康則：「有限要素法による速度項のある電磁場解析の検討」，電気学会回転機・静止器合同研究会資料 RM-85-44，SA-85-53

　
解析モデル

図１に解析モデルを示します。導体は速度 Vx で x 方向に移動していますが， 定常状態を仮定していますので１回の定常解析により解を求めます。

　　　

　

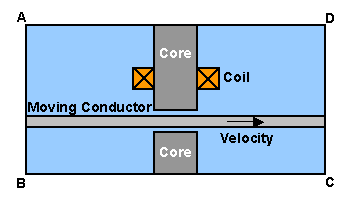
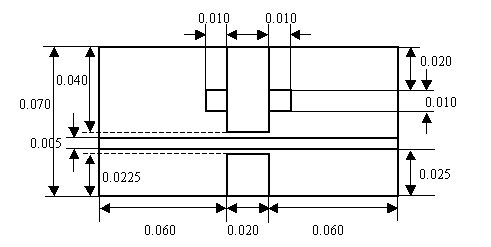
図１　解析モデル　（寸法の単位は m ）

 　
解析条件
材料 空気，コイル
比透磁率 1.0
材料 導体
非透磁率 1.0 ，電気抵抗率　4.31E-08[Ωm]　（導電率：2.32E+07 [S/m]） ，移動速度：パラメータ
材料 鉄心コア

比透磁率 500.0（一定値)
励磁電流
右側コイル部 −1000 [AT] （駆動電流密度：‐1.0E+07 [A/m2]）
左側コイル部 ＋1000 [AT] （駆動電流密度：+1.0E+07 [A/m2]）
境界条件
 AB，CD境界上：ベクトルポテンシャル 0
BC，DA境界上：自然境界条件

　

　
解説
２次元直流定常場運動解析の支配方程式は以下のようになります。

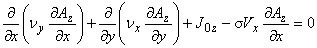
導体の渦電流密度は次式で計算されます。

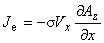
速度起電力を表す項は，流体解析などでいう移流項に相当します。
移流項が支配的な現象を数値解析するためには，安定的に解析を行うために，離散化に対して特別の配慮をする必要があることが知られています。
ガラーキン法による離散化では，運動を考慮した解析においては，次式で定義されるペクレ数 Pe < 1 であることが安定的に解析できる指標とされます。

ここで，
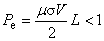
μ：透磁率
σ：導電率
V：導体の移動速度
L：移動方向のメッシュ辺長

解析は，導体の速度を
0.0 [m/s]
1.0 [m/s]
30.0 [m/s]
100.0 [m/s]
1000.0 [m/s]
とした5つのケースについて行います。
結果は磁束線分布，渦電流密度分布，導体表面ポテンシャルグラフを求めます。

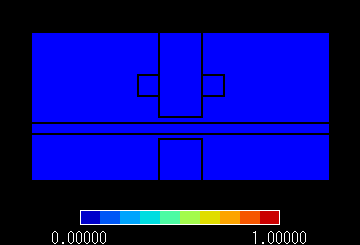
図２にメッシュ図を示します。 本問題は文献に近い分割数を目指し三角形1次要素を使用し，要素数は896です。
（文献では，四角形１次要素が使用されています)

 　
メッシュ

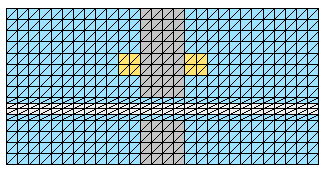
図２　メッシュ図

 　

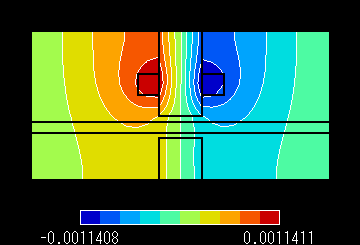
解析結果　磁束線分布（左）　渦電流密度分布（右)
　
図３ A　速度 0.0 m/s Pe：0.000　磁束線分布
　
　
図３ B　速度 0.0 m/s Pe：0.000　渦電流密度分布
　

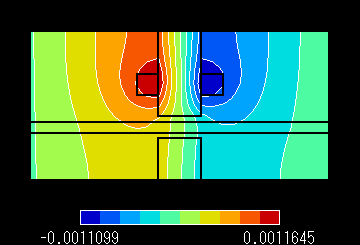
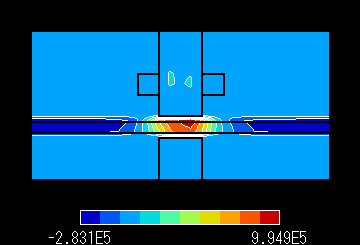
図４ A　磁束線分布　速度 1.0 m/s Pe：0.070
　
　図４ B　渦電流密度分布　速度 1.0 m/s Pe：0.070

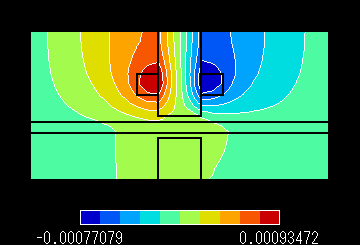
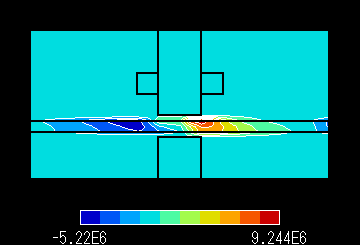
図５ A　磁束線分布　速度 30.0 m/s Pe：2.102
　
図５ B　渦電流密度分布　速度 30.0 m/s Pe：2.102

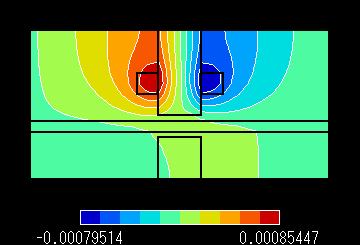
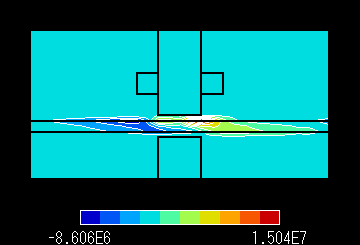
図６ A　磁束線分布　速度 100.0 m/s Pe：7.006
　
図６ B　渦電流密度分布　速度 100.0 m/s Pe：7.006

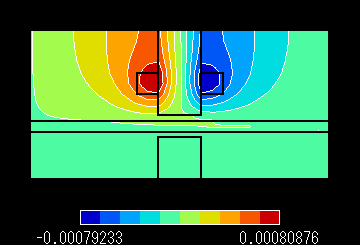
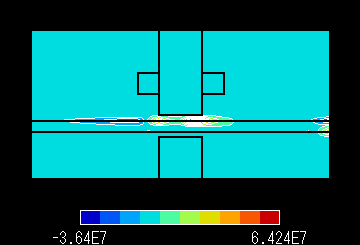
図７ A　磁束線分布　速度 1000.0 m/s Pe：70.058
　

図７ B　渦電流密度分布　速度 1000.0 m/s Pe：70.058
　

　　

解析結果　導体表面上のポテンシャル分布

　

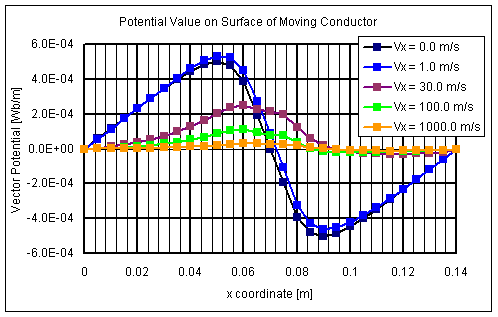
図８　速度が大きくなるにつれて移流の影響が大きく現われてきます。

　

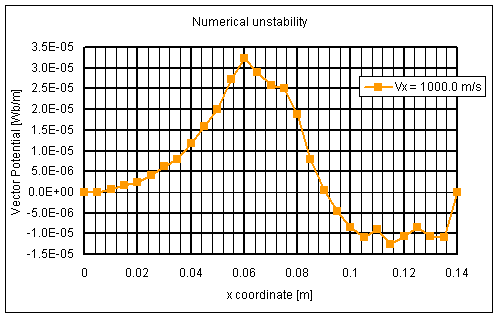
図９　速度が大きくなるとペクレ数が１より大きくなるので風下側で数値不安定性が顕著に現われてます。

以上より通常のガラーキン法では導体の移動速度が大きくなってくると解析がうまく行えなくなります。
これを回避するためには，上流化を施した風上有限要素法による定式化を行なうか，運動物体上に座標系をとる方法などが提案されています。なお速度項のある解析は生成されるマトリックスが非対称になるため，ICCG法ではなくPCGS法というソルバーを実装し使用しました。