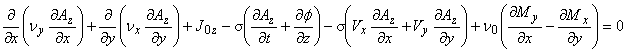2 次元磁場解析 NO.1 / 2次元磁場解析の支配方程式
マクスウェルの方程式は次の 4 つの式で表されます。
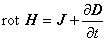
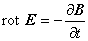
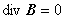
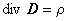
ここで,B は磁場[T],E は電場[V/m],H は磁界[A/m], J は駆動電流密度[ A / m2 ],D は電束密度です。
式(1.1)は,アンペールの法則であり,電流が流れると周囲に磁界 H [A/m] を誘導することを示しています。
式(1.2)は,ファラデーの電磁誘導の法則であり,磁場 B [T] が時間的に変化すると
周囲に電場 E を誘導することを示しています。
式(1.3)は,磁場 B [T] の保存を表す式です。これは,磁束線は常に連続であるという意味です。
式(1.4)は,電荷の保存を表す式です。
以上 4 つの式に続いて,次の 3 つの構成方程式を考えます。
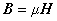
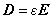
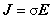
1 [H] = 1 [ Wb / A ] = 1 [ m2kg / A2 sec2 ]
1 [ H/m ] = 1 [ Wb / A m ] = 1 [ m kg / A2 sec2 ]
1 [F] = 1 [ C / V ] = 1 [ A2 sec4 / kg m2 ]
1 [ F/m ] = 1 [ C / V m ] = 1 [ A2 sec4 / kg m3 ]
1 [S] = 1 [ A / V ] = 1 [ A2 sec3 / kg m2 ]
1 [ S/m ] = 1 [ A / V m ] = 1 [ A2 sec3 / kg m3 ]
異なる媒質 1 〜 2 における境界条件は,次の5つの式で与えられます。 準定常磁場解析では,特に式(1.10)と(1.11)が重要です。
この 2 式は不連続境界で,磁場 B [T] については境界面の法線成分が, 磁界 H [A/m] については接線方向成分のみが連続であれば良いことを示しています。

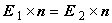
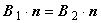
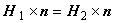
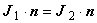
一方,低周波問題では時間微分項は無視できるので,静電場問題と静磁場問題に分離され, 式(1.1)または(1.2)のどちらか一方を解く準定常問題へと縮小されることになります。
解析領域内に,永久磁石ではない強磁性体があり,渦電流を無視した静磁場問題について考えます。 10 MHz 以下の低周波数領域において マクスウェル方程式(1.1)の変位電流の項は無視してよいので, 式(1.1)で時間微分項を無視した式と式(1.3)の 2 つの式を考えます。
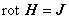
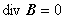
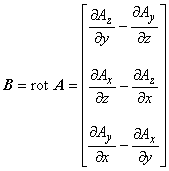
となるような磁気ベクトルポテンシャル A [ Wb / m ] を定義することができます。
*電流が流れるとその周囲に磁場が誘導されます。
磁束線は電流源に対して渦状に生じますので,磁束線は必ず始点と終点が同じ点となりループを形成します。
したがって,必ず,div B = 0 となります。(モノポールの不在)
*一般に,あるベクトル場 X が別のあるベクトル場 Y によって X = rot Y と 表されるとき Y を X のベクトルポテンシャルといいます。
よってベクトルの公式
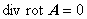
ここで,任意のスカラーポテンシャル φ の勾配を加えた新たなベクトルポテンシャル A’ を次式のように定義します。
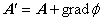
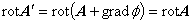
すなわち,この時点では A に関するベクトル場が一意に定まっていないことを意味しています。 一般的にベクトル場が一意に定まるためには,回転と発散が与えられる必要があります。 ここでは回転のみが与えられているので,発散(ベクトルポテンシャル A が連続であるという条件) を次の式で与えます。
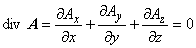
以上の操作をゲージ変換といい,ここで与えた発散条件のことをクーロンゲージ条件といいます。
ここで特に注目すべきことは, 2 次元場では次の 2 つの仮定がなされるということです。
1: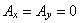 であること
(補足3)
であること
(補足3)
2:z 方向には, A は変化しないこと ---> dA / dZ = 0
以上の仮定により,2次元場ではクーロンゲージ条件が自動的に常に満足されます。 したがって、一般的に 2 次元解析ではゲージ条件を意識することなく解析することが可能です。
以上より 2 次元問題に関しては,A に関するベクトル場が一意に定まることがわかりました。
次に駆動電流による静磁場の支配方程式を導きます.
駆動電流とは,外部電源より導入される電流のことで,磁場変化に伴い磁性体に誘起される渦電流や,
磁性体の磁化モデルから仮定される磁化電流と区別して下さい。
一般には,単に電流ということのほうが多いでしょう。しかしながら,磁場解析では解析モデル
(これを系と呼ぶことにします)になんらかの入力があって,それに対して系がどのような応答をするかを考えます。
入力とはここでは,外部電源より供給される電流のことです。
磁場は電流が流れることで生じることはマクスウェル方程式より自明です。
すなわち磁場の入力は電流であり,磁場という系を駆動させることから駆動電流と表現しているのです。
式(1.5)を磁気抵抗率を用いて次のように変形します。
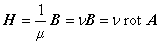
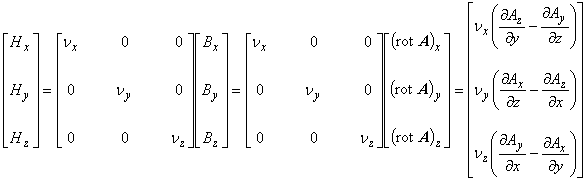
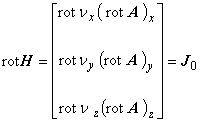
渦電流は導体や磁性体に鎖交する磁束が変化した場合に現在の磁束を維持するように流れます。
具体的には,駆動電流が時間的に変化しそれに伴い磁場が変化するような場合と, 磁場中を導体や磁性体が運動する場合があげられます。
渦電流密度 Je は,構成方程式(1.7)に速度項を導入した次の式で表されます。 V は導体の運動速度です。
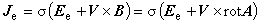
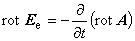
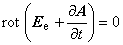
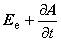
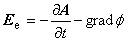
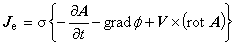
ただし,
磁束の時間的変化がない場合:dA/dt = 0 , grad φ = 0
渦電流が生じる磁性体や導体の速度が 0 の場合:V × rot A = 0
となります。
この場合,磁場 B [T] と,磁界 H [A/m],磁化 M [T] の関係は次の式で表されます。
磁石などを扱う磁気工学分野では,上で M [T] とした物理量のことを, 磁気分極あるいは磁化と言い I [T] や J [T] で記述されますが, 有限要素法の分野でこれらの文字は, 電流値の I〔A〕や電流密度ベクトルの J〔A/m2〕と混同するため, M [T] と いう文字を採用しています。
この M [T] に相当する物理量の定義が統一性を欠いている事態については, 磁性体を扱う勉強や研究のあらゆるシーンで深刻な混乱を招いており,読者は文献およびソフトウェア等が どのような定義を採用しているか十分チェックしてください。
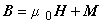
B = μ0 H + M
M の単位は [T] つまり磁荷をイメージ。
と定義していますが,最近では次のような定義のほうがより一般的です。
B = μ0( H + M )
M の単位は [A/m] つまり磁化電流をイメージ。
式(1.28)を,次のように磁界 H [A/m] について表す式に変形します。
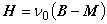
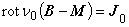
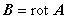
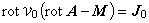
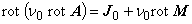
すなわち,
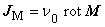
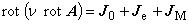
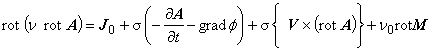
| 空気領域 | 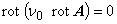 |
(1.36)
|
| コイル領域 | 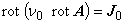 |
(1.37)
|
| 永久磁石領域 | 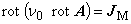 |
(1.38)
|
| 渦電流のある磁性体 | 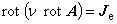 |
(1.39)
|
| 常磁性導体領域 | 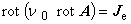 |
(1.40)
|
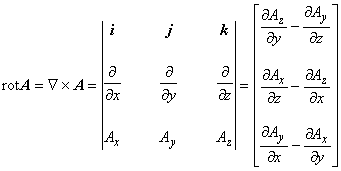
静磁場項の成分を求めてみます。まずベクトルポテンシャル A の回転をとります。
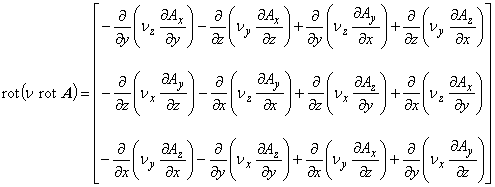
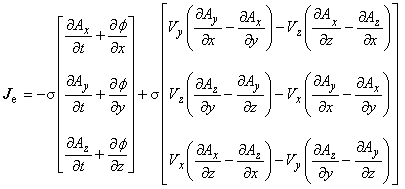
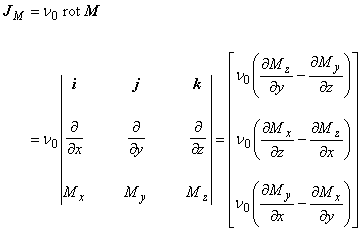
以上より各項に関する準備ができました。
支配方程式の成分表示は以下のようになります。
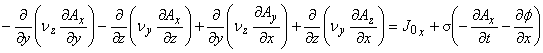
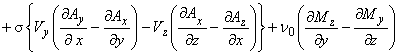
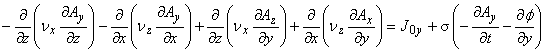
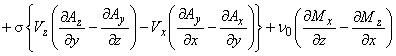
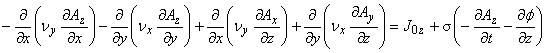
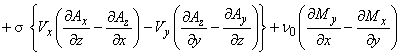
したがって計算コストは非常に大きくなります。
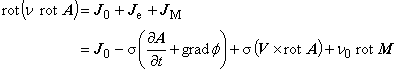
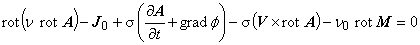
これは,ベクトルポテンシャル A および電流密度ベクトル J が, z 方向成分のみを有することを意味します。
すなわち,

および z 方向一様という仮定により,2次元場での支配方程式は次のように表されます。