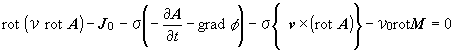
(1.1)
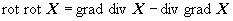
(1.2)
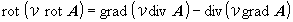
(1.3)

(1.4)
このことはベクトル場が一意に定まっていないことを示しており,このまま微分方程式を解こうとするとφの数だけ解が得られます.φは任意の数ですから事実上,解は無限に存在することになります.
そこで,電磁気学的にはゲージ条件を課してベクトル場を一意に決定するゲージ変換を行ないます.これには次式で表されるクーロンゲージがよく用いられます.
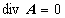
(1.5)
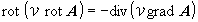
(1.6)
この結果,常にただ一つのベクトル場の解が得られることになります.
しかしながら,数値磁界解析においてクーロンゲージなどによる電磁気学的なゲージの固定は意図的に行なわないのが普通です.クーロンゲージを課した場合,方程式の整合性をとるためにペナルティ項を付加し,節点に未知数を割り付けた通常の有限要素法の要素である「節点要素」で離散化して得られる解は,
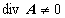
(1.7)
になることが知られているからです.したがって,一般的には電磁気学的なゲージ変換は行なわずに定式化を行います.これより,微分方程式を解いて得られる磁気ベクトルポテンシャルAは一意ではありませんが,そこから得られる磁束密度Bは常に一意であることがわかっています.
重み関数に要素の補間関数{N}を採用すると,式(1.1)にガラーキン法を適用した式は次式のようになります.
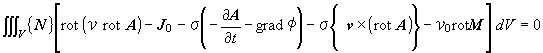
(1.8)
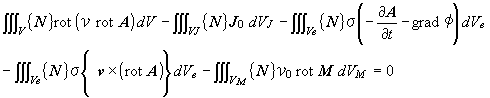
(1.9)
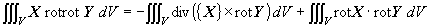
(1.10)
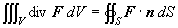
(1.11)
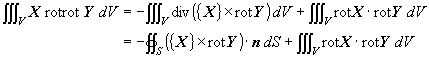
(1.12)
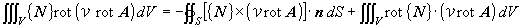
(1.13)
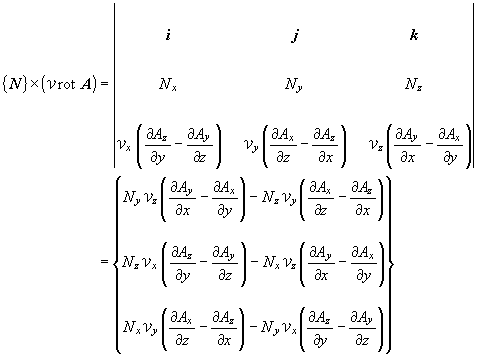
(1.14)
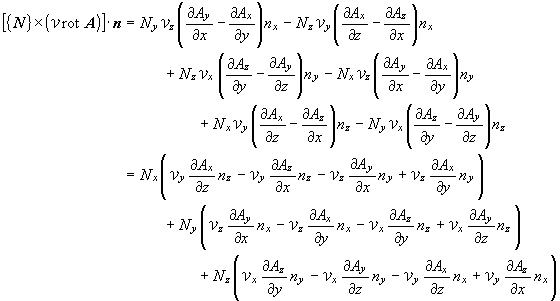
(1.15)
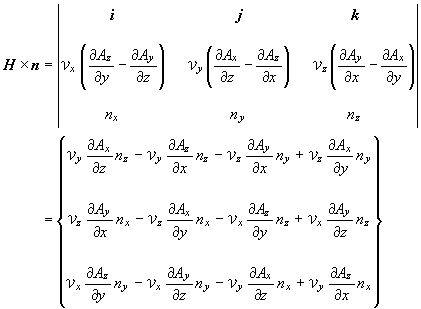
(1.16)
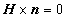
(1.17)

(1.18)
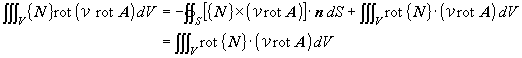
(1.19)
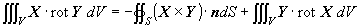
(1.20)
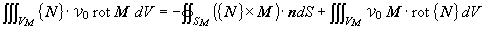
(1.21)
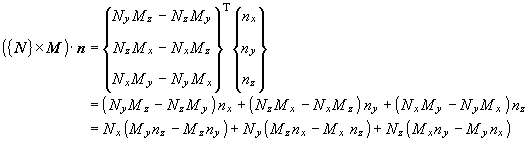
(1.22)
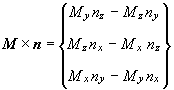
(1.23)
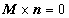
(1.24)
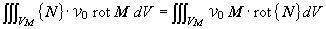
(1.25)

